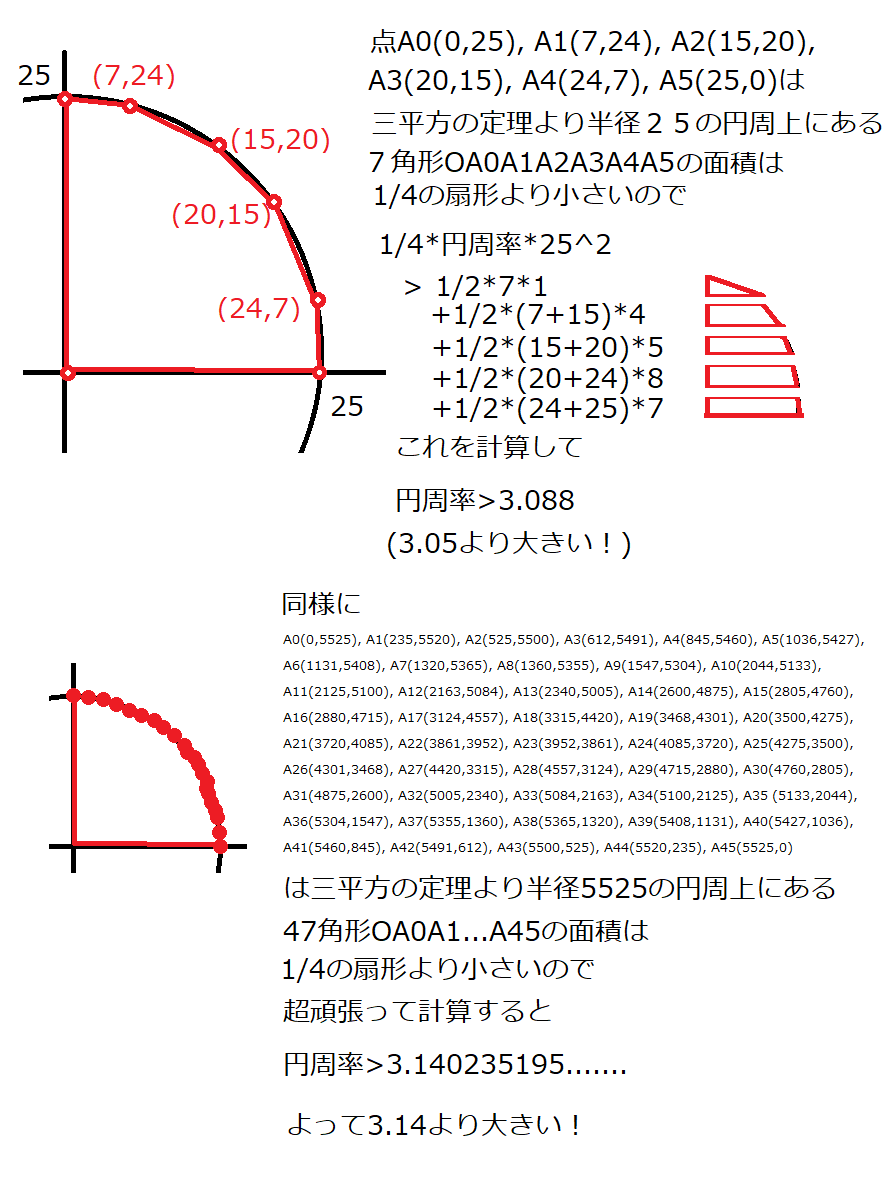
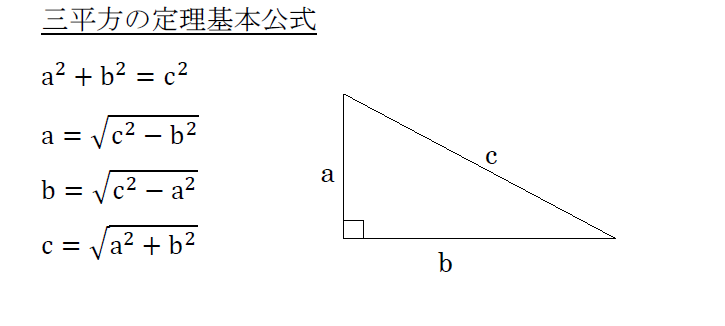
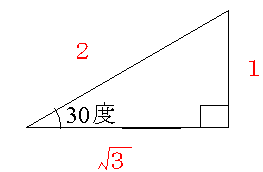
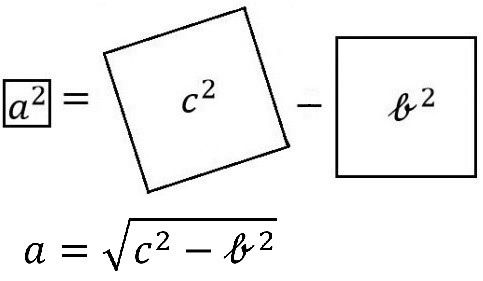
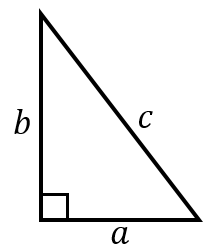
受験勉強のコツです。 受験の数学で必須項目の一つに「三平方の定理」があります。 a 2 b 2 = c 2 です。 (ここで、直角に対する辺cが斜辺です。 ) 図1:直角三角形。 90゜に対する辺cが、斜辺。 さらに、応用問題でよく利用される辺の比があります。
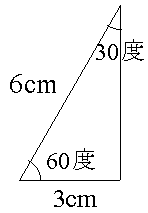
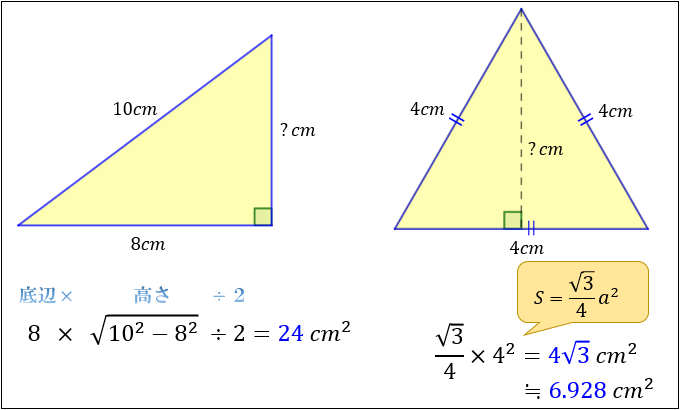
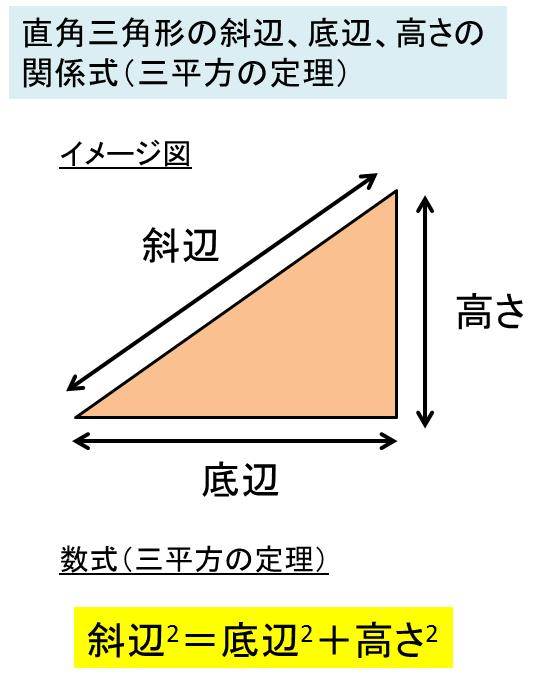
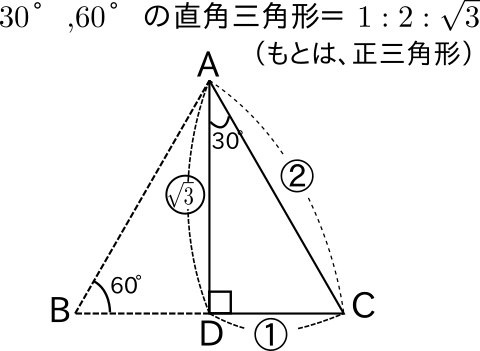
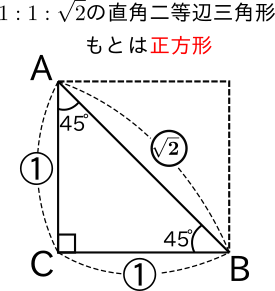
三平方の定理 ルートを含む- 三平方の定理で覚えておきたいのは、 直角三角形の比 だよ。 これを覚えておけば、 三平方の定理を使わなくて辺の長さを計算できちゃうんだ。 楽に解けるんなら知っておきたいよね? んで、そのパターンは全部でつぎの3つ。 30、60の直角三角形;三平方の定理とは、直角三角形において 斜辺の長さの2乗は、他の辺の長さの2乗の和に等しくなる。 というものです。 文章だけでは、難しく見えますが 非常に単純な定理です。 このように 斜辺の2乗の数と 他の辺を2乗して足した数が等しくなるのです。 直角三角形であれば、必ずこう
三平方の定理 ルートを含むのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | 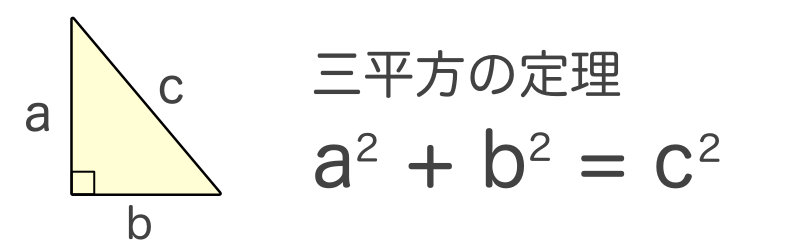 |
 |  |  |
 | ||
「三平方の定理 ルートを含む」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
 |  |  |
「三平方の定理 ルートを含む」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
 |  | |
「三平方の定理 ルートを含む」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
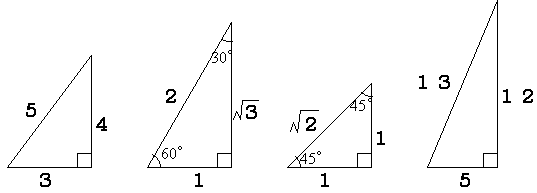 |  |  |
「三平方の定理 ルートを含む」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  | |
「三平方の定理 ルートを含む」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  | |
「三平方の定理 ルートを含む」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  |  |
「三平方の定理 ルートを含む」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 | ||
「三平方の定理 ルートを含む」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |
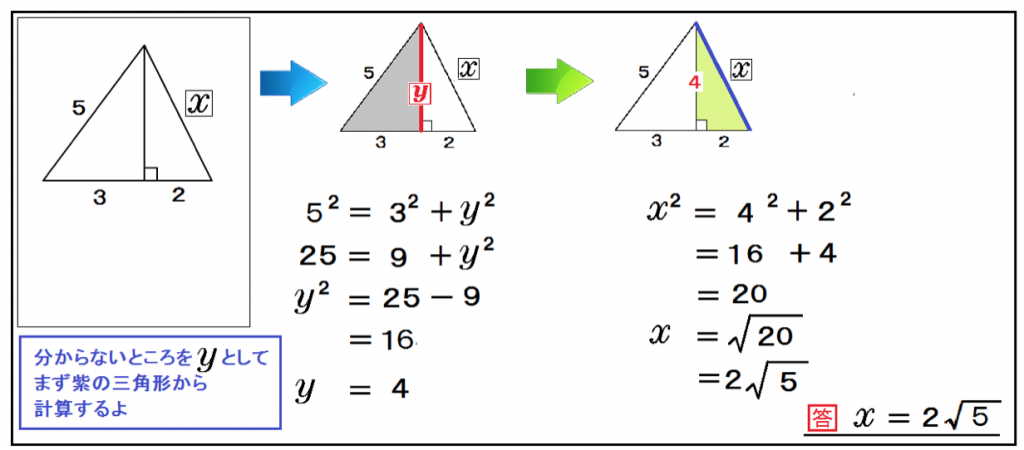
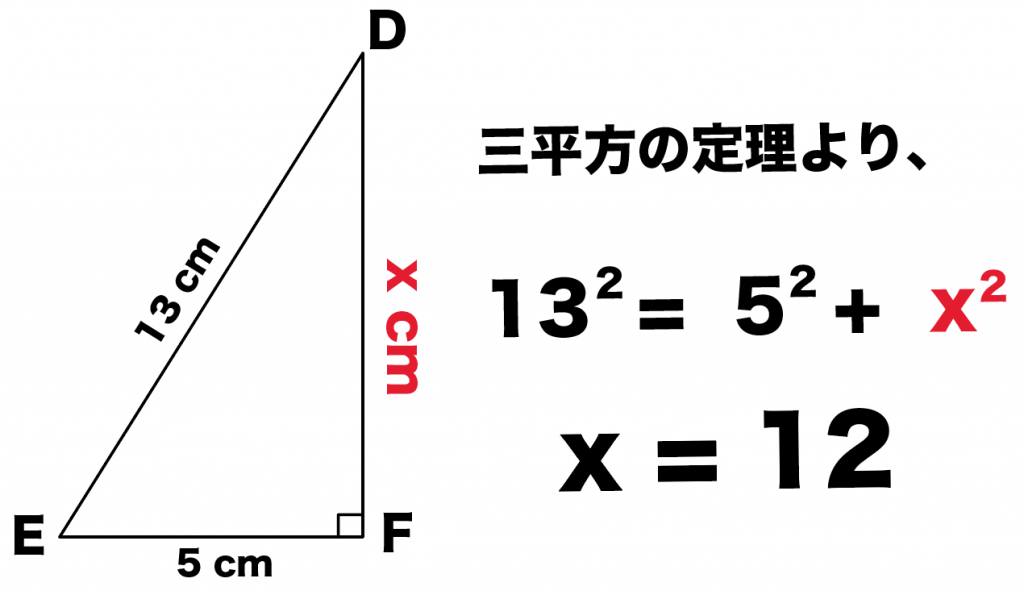
まぁ、三平方の定理でも解けますね。 しかし、もし、4ではなく04などの小数や分数が出た場合は、ちょっと計算が苦しくなります。 あくまでも、一時しのぎと考えて使ってください。 本来は、 比を利用するのがベスト です。 Tweet ← 受験数学:三平方 三平方の定理(ピタゴラスの定理)を使えば求められるんだ。 DFの長さをxcmとして、三平方の定理(ピタゴラスの定理)に代入してみると、 13² = 5² x² x = 12 あら不思議! 長さがわからない直角三角形の辺を求めることができたね。 >> 三平方の定理
Incoming Term: 三平方の定理 ルート, 三平方の定理 ルート なぜ, 三平方の定理 ルート 解き方, 三平方の定理 ルート3, 三平方の定理 ルート5, 三平方の定理 ルートを含む,



