約分の裏技 分母と分子の 差 から、 公約数を推測 する。 例題では、分子 299 と分母 437 の差ですので、 437 – 299 = 138 この 138 の 約数 を考えましょう。 約数を求めるときは、逆さ割り算を使います。 よって、 138 = 2 × 3 × 23 これより、元の 299 と 437 の約分の意味 分数の問題は小学校だけでなく中学・高校・大学までずっと出題されつづけますが、常に付きまとう暗黙のルールが 「分数は分母・分子が互いに素な数になるまで(公約数がなくなるまで)約分しないといけない」 というものです。 分数には「分母と分子に同じ数をかけたり割っ足し算(真分数のみ、分母が異なる) 引き算(真分数のみ、分母が異なる) 足し算(3つの真分、数分母が異なる) 引き算(3つの真分数、分母が異なる) 足し算(帯分数を含む、分母が異なる)
簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
分数 足し算 約分する
分数 足し算 約分する-分数の足し算・引き算の手順 通分する(分母を揃える) 分子同士を計算する なぜ通分しなければいけないのか? たとえば分母が等しい時を考えてみると、計算は普通の足し算・引き算と同じ要領でスムーズにできるのがわかります。 分母が同じという分数の足し算 😙 それと何度も言ってますが最後の約分は忘れないようにしましょう。 分数の足し算の解説 分数の足し算をおこなう場合、分母が違うと単純に数を足すことはできません。




小学3年生 算数 無料問題集 分母が同じ分数の足し算 おかわりドリル
無学年で分数に関する演習をする計算プリントです。 進級テストつき! 分数計算トレーニング (無学年) ・仮分数⇔帯分数 ・等しい分数 ・倍数/公倍数 ・約数/公約数 ・約分/通分 ・同分母たし算/引き算 ・分数のたし算/引き算 ・分数のかけ算 ・分数のわり算 ・10回のテスト形式で計算力をGeoGebra で 例題1 と 例題2 を解いた画面です。グラフは不要ですが,約分と足し算の計算ができています。 繁分数を簡単にする 次に 繁分数 の扱い方を覚えましょう。繁分数と言うのは \\displaystyle \frac{1 \displaystyle\frac{x 1}{x 1}}{1 \displaystyle\frac{x 1}{x 1}}\ 分数の足し算・引き算・掛け算・割り算のやり方を一覧にまとめました。 それぞれの計算の仕方を忘れてしまった場合は、こちらで確認しましょう。 (基本的な問題もあわせて練習できるようになっています。) 分数の足し算やり方と問題 分数の引き算やり方と問題 分数の掛
分数足し算 問題テーマ 分母が同じ1以下の足し算 分数足し算約分なし 分数の足し算・解1まで (分母5まで) 分数の足し算・解1まで (分母9まで) 分数の足し算 (分母6まで) 分数の足し算 (分母9まで) 分数の足し算 (分母2桁1) 分数の足し算 (分母2桁2)考え方と答え 帯分数が混じった足し算では、整数部分どうしと、真分数どうしをそれぞれ別に足し算した後で、さらにその和を考えればいいよ。 (1) 1/5 と 2/5 の真分数どうしを足すと、 3/5 。 1と1/5 の1をそれに足して、 1と3/5 。 ※ 1と3/5 は、 1 + 3/5 という意味だよ。 分数×分数の計算は、〈例題1〉で紹介したやり方と同じです。分母は分母同士かけ算、分子は分子同士かけ算しましょう。 ③約分 〈例題5〉 分数の計算が終わったあとは、「約分」をする必要があります。
分数とは? ある数を0でない他の数で割った商を、横線の上に割られる数、横線の下に割る数を表したものです。 分数の足し算 通分(分母を同じにすること)します。分子同士を足し算します。約分します 分数の引き算 通分(分母を同じにすること)します。分数の足し算・引き算を初めて習う子に向けた学習プリントです!分母が同じ分数どうしのたし算・ひき算の学習プリントです。約分などはありません。(例:4/6 + 9/6 = 13/6) 第 6 回のテーマは「 分数の概念と計算方法 」です。 割り算 , 割合 , 比の「 変形 」である「 分数 」についての話です。 今までの「 割り算 , 割合 , 比 」の知識 は、この「 分数 」を理解することで 全てが繋がり、完成します 。 分数は小数とも密接な関わりがあります。




中1数学 正負の数 分数計算のやり方を問題解説 数スタ




最高の分数 整数 足し算 子供のための最高のぬりえ
技能 約分,通分や異分母の分数の加法及び減法の計算をすることができる。 知識・理解 分数の性質や約分,通分の意味,異分母の分数の加法及び減法の意味や それらの計算の仕方について理解する。 4 単元の指導計画(11時間) 時 ☆500枚☆ 分数の足し算引き算をしてください。早くて正確な方にba 約分もできる場合はしてください。 ①8分の1+2分の1= ②10分の1+5分の2= ③4分の5+12分の1= ④15分の2+6分の7= ⑤2と4分の1+3と10分の3= ⑥1と12分の11=4と分の7= ①4分の1-分の3= ②6分の5-18分の7= ③14分の25-6分のこの分数の性質を利用して、 分母・分子を同じ数で割って、分母と分子を最小の分数にすることを 約分 (やくぶん) と言います。 約分の方法 約分をおこなう方法としては、まず基本的な方法として分母・分子を同じ数で割っていき割り切れなくなるまで繰り返すという方法があります。




練習問題 3分でできる ルート分数の足し算 引き算 Qikeru 学びを楽しくわかりやすく




144たし算 整数 分数 約分 Youtube
①異分母分数の足し算場面 ③「約分」→次の分数を約分しましょう。 ①分数の掛け算が用いられる場面 ①「~しない~な~。」→ここで約分しない簡単な方法。 ②分数の掛け算の方法(分数×整数) ②「長方形」「縦・横」「広さ」 ①分数の割算が分数とは、ある数を 0 でない他の数で割った商を、横線の上(分子)に割られる数、横線の下(分母)に割る数を記して表したものです。 このページでは、分数の計算のやり方をまとめています。各項目では、加減乗除の四則計算について、それぞれの計算方法と簡単な計算例をご紹介してい分数の足し算 小学生5年生の算数 分数の約分 分数の約分です。「毎回異なるプリントが作られます」をクリックしてダウンロードできます。 印刷枚数を指定する場合は、下で枚数を指定してくださ



分数の足し算の世界初の説明方法 小僧の裏紙ブログ 楽天ブログ



1
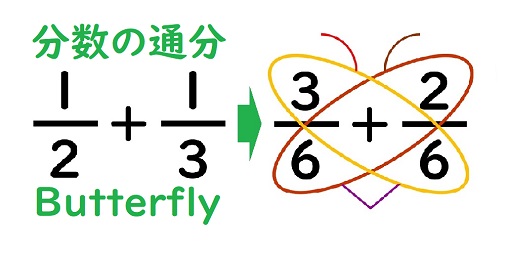
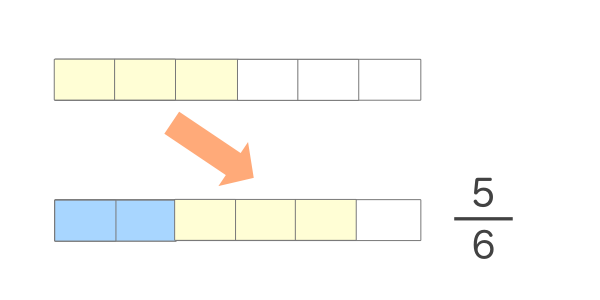
それぞれを同じ等分に変えてやることで、計算がイメージしやすくなるよね。 このように、 分母を揃えて同じ等分にかえてやる こと。 これを 分数の通分 といいます。 基本的には、 それぞれの分母にある数の最小公倍数で揃えていきます。 それでは、分数の通分について手順を追って分数は 比 や 割合 といった概念に対応しており、0 でない数 a を分母と分子にそれぞれかけても割っても、その分数の表す数は変わらない。 n m = n × a m × a = n ÷ a m ÷ a ( a ≠ 0 ) {\displaystyle {n \over m}= {n\times a \over m\times a}= {n\div a \over m\div a}\quad (a\neq 0)} m と n 分数の足し算 分数の足し算は ①:2つの分数の「分母」が同じになるようにそろえて(通分して)から ②:2つの分数の「分子」を足し算をして ③:最後に「約分」をする。 この 3つのステップをふむのがコツ です。 ここでは、「2/3 1/12」を計算してみましょう。



分数の足し算 簡単に計算できる電卓サイト
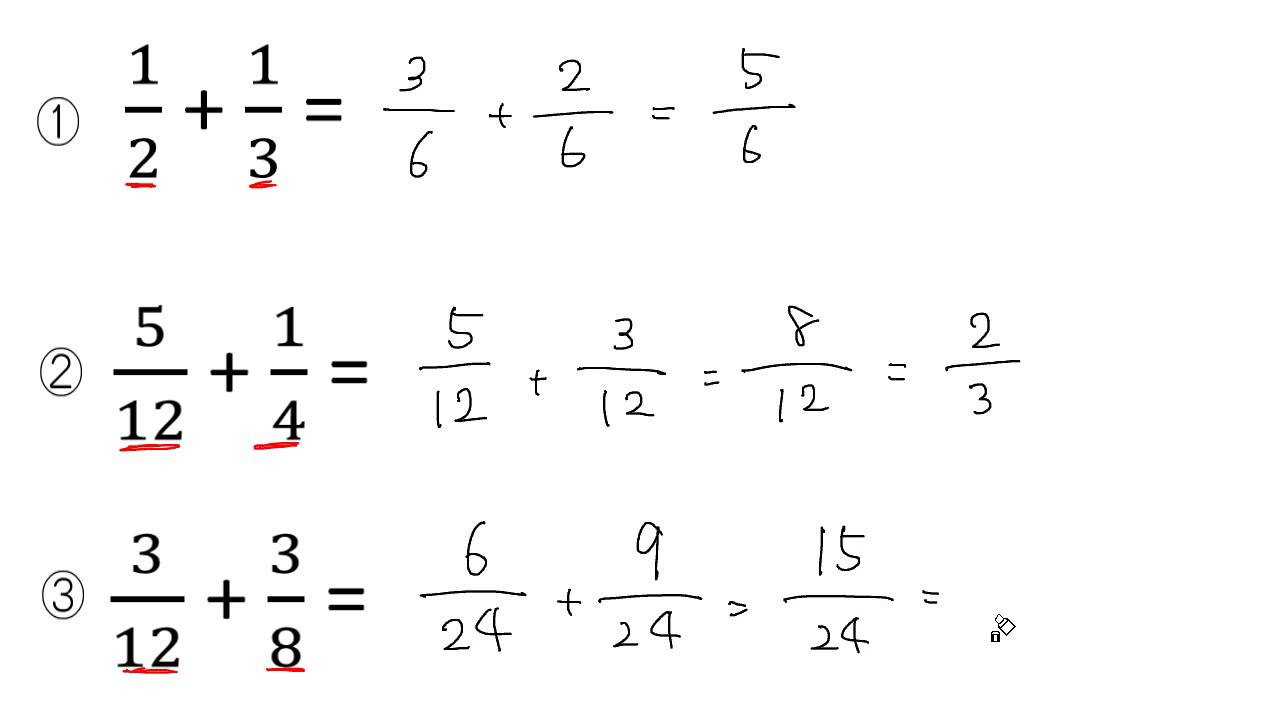



分数の足し算 引き算 通分あり Youtube
分数の足し算で「約分」が発生する条件 (2) 早速ですが、昨日の記事の続きです。 tsujimotterhatenablogcom 前回の記事では、分数の足し算の計算で約分が発生する条件について考えました。 特に、結果の分母・分子が素数 で約分されるならば、 が で注意 問題も答えも約分していない数です また計算 結果が仮分数の場合は答えは 整数か帯分数に直して答えましょう。 帯分数と仮分数の足し算 整数の部分が2桁になる計算 問題1 ・ ・ 1ページ14問 問題4ページ、答え4ページ5年算数分数(1)通分約分の教え方 この勉強には 「公倍数・公約数」の完全な理解 が必要です。 理解不十分なお子さんには、まず こちら (公倍数・公約数) でおさらいさせましょう。 ① 等しい分数の意味とつくり方 ② 約分・通分の意味と約分・通分の
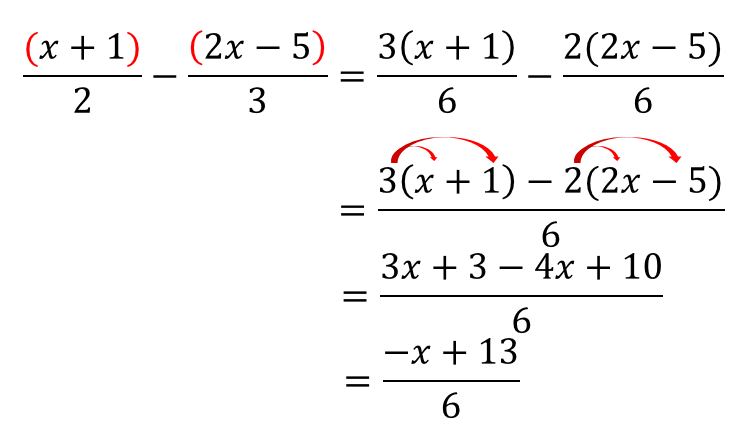



文字式 分数の計算問題を1から丁寧に 数スタ




やり直し算数小5 分数の足し算引き算 約分がある場合 Youtube
この方法を使えば、約分せずにそのまま分数を表示することができますね。 また、 分数によって余りが出る場合は通常、帯分数になります 。 仮分数・・・分子が分母より大きい場合、そのまま上に書く・・・3/2 帯分数・・・分子が分母より大きい場合
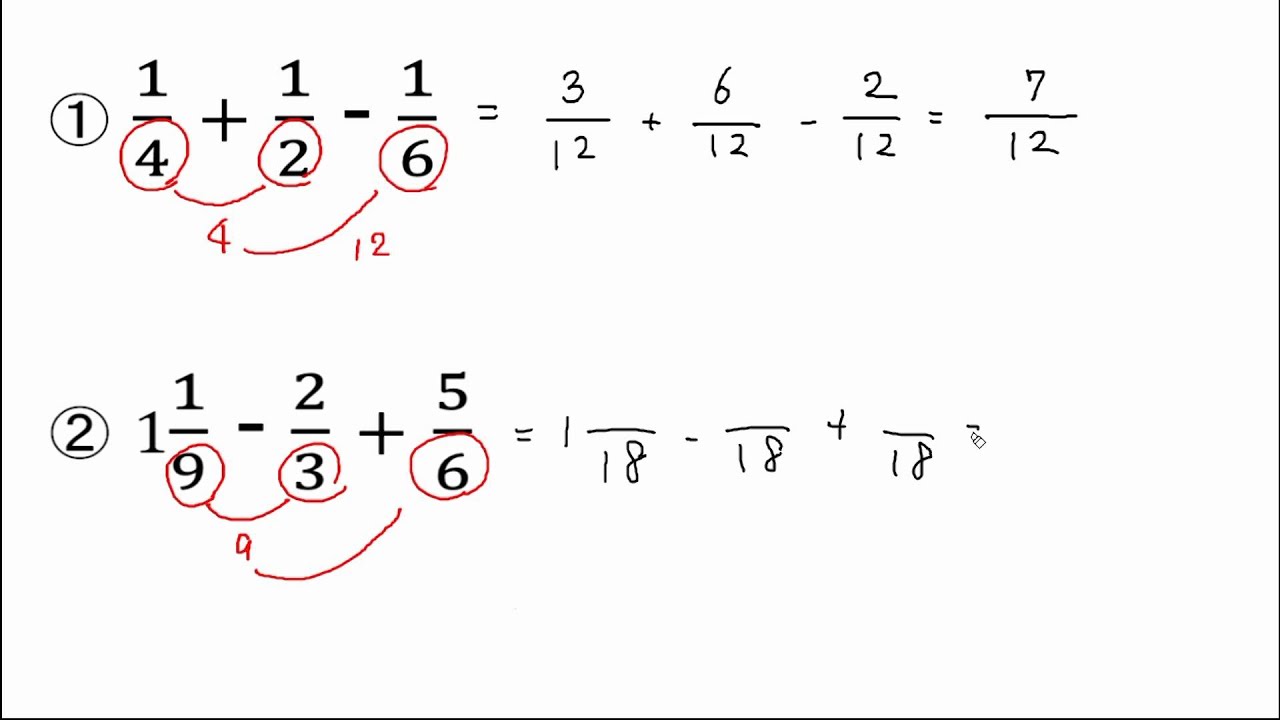



足し算とひき算が混じった分数の計算 Youtube
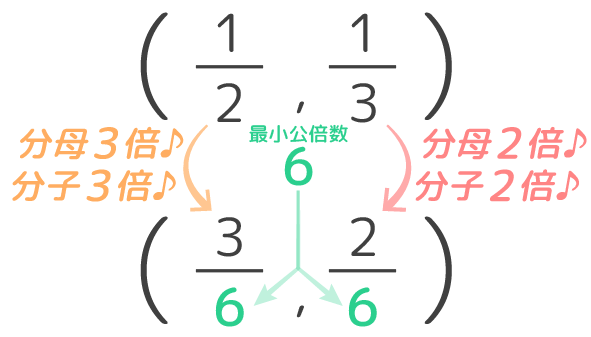



何年生で 分数の通分のやり方教え方と問題演習 3つの分数の通分も そうちゃ式 分かりやすい図解算数 別館




小学5年生 算数 無料問題集 分母が違う帯分数の足し算 おかわりドリル




異分母の足し算のやり方 大人の学び直し算数 計算のやり方解説 無料




無料印刷可能分数 足し算 引き算 問題 子供のための最高のぬりえ




分数の足し算 引き算は通分してもしなくても同じ値 Okwave




โน ตของ 分数の足し算 約分 ช น Primary算数 Clear




みのすけママの母さんな日々 分数の計算 掛け算と割り算のどちらを使いますか




分数の多項式の足し算や引き算 通分してからがポイントだ 中学や高校の数学の計算問題




分数の約分のやり方と教え方のコツ 時間短縮に便利なテクニックを紹介 数学fun
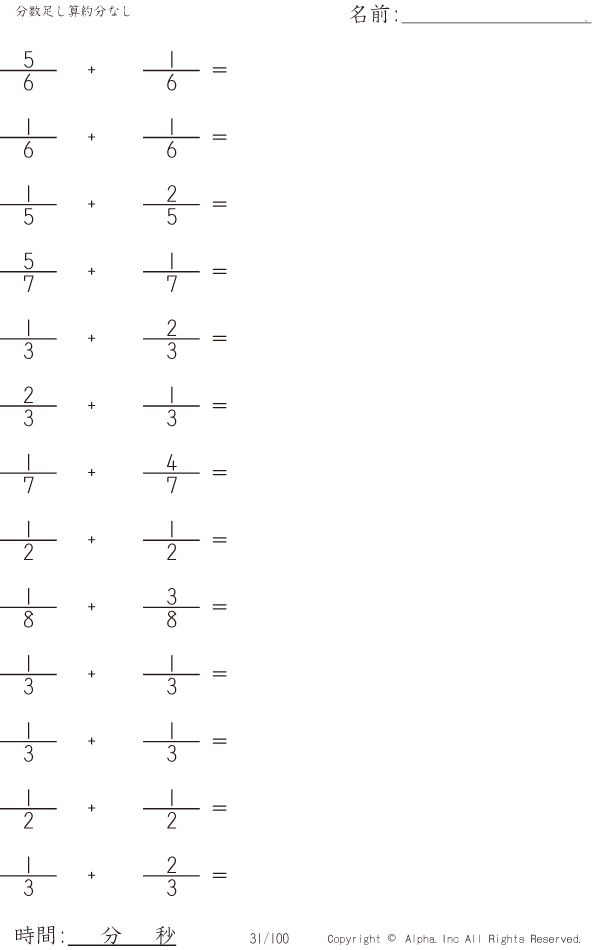



分数足し算約分なし 問題 031 100



1
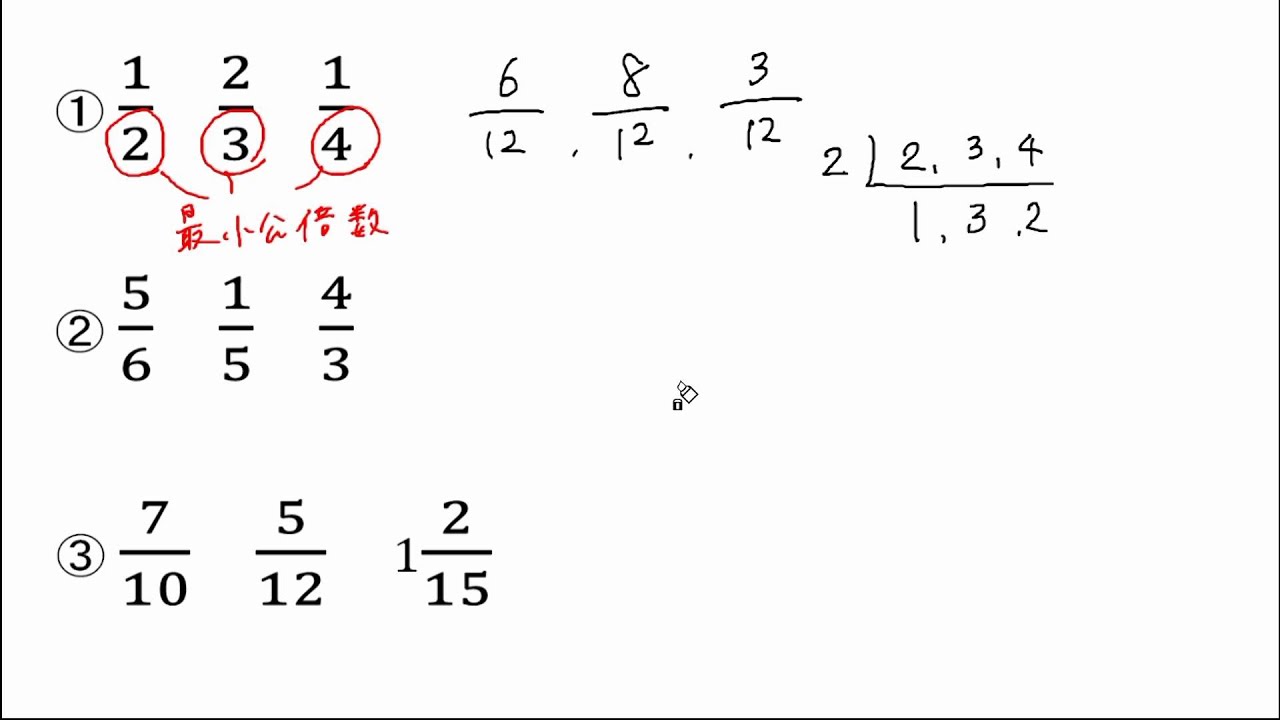



通分 問題練習 Youtube




帯分数の足し算の計算プリント 分母が同じ問題 全240問無料 算数パラダイス




小学5年生の算数 異分母の分数の足し算 練習問題プリント ちびむすドリル 小学生




小学3年生 算数 無料問題集 分母が同じ分数の足し算 おかわりドリル



異分母の引き算のやり方 大人の学び直し算数 計算のやり方解説 無料




算数 分数の足し算 Youtube



分数 文字式 約分
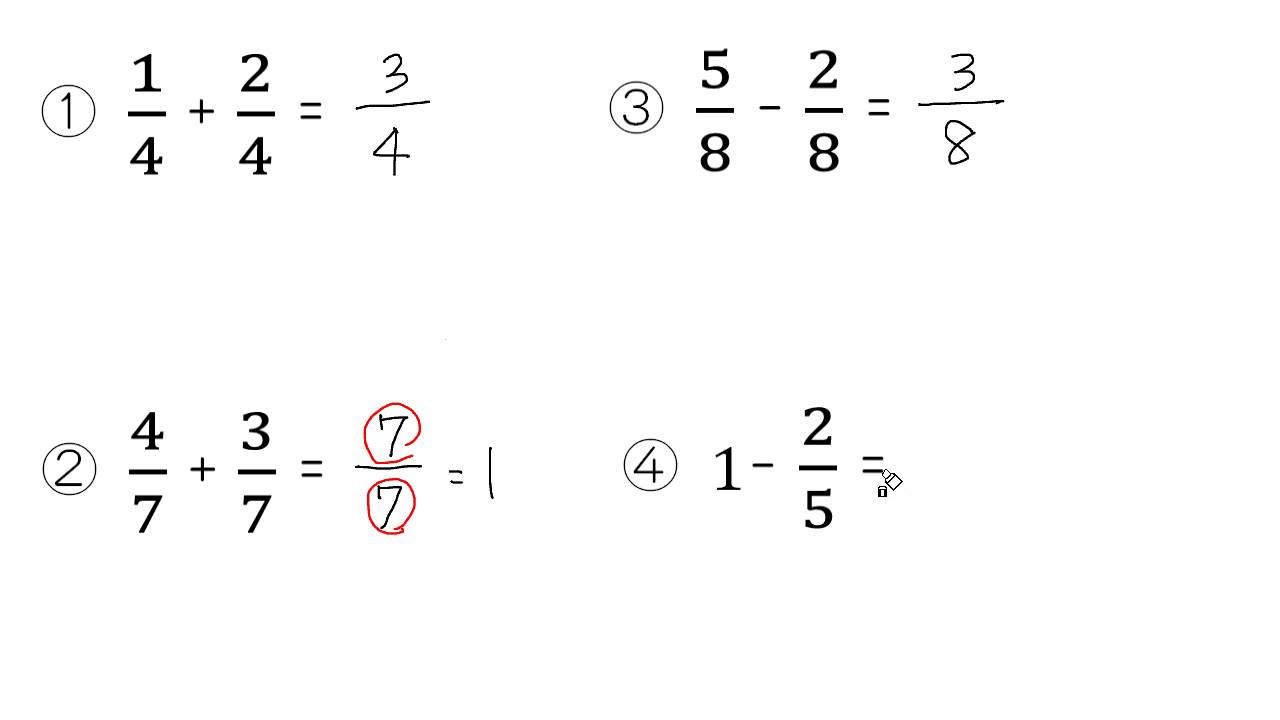



分数の足し算 引き算 練習 Youtube



ドリルズ 小学3年生 算数 の無料学習プリント分数の足し算 引き算




分数 分数の約分 中学生からの勉強質問 数学 進研ゼミ中学講座




分数のかけ算の問題 やり方は簡単だが 約分に気をつけよう 中学や高校の数学の計算問題




5年生 分数の足し算 引き算 まなび365 小学生の算数プリントを自動作成 無料で自宅学習




初等代数 分数を教える 通分 約分 足し算 大人が学び直す数学



小数と分数が混じった式の解き方 大人の学び直し算数 計算のやり方解説 無料
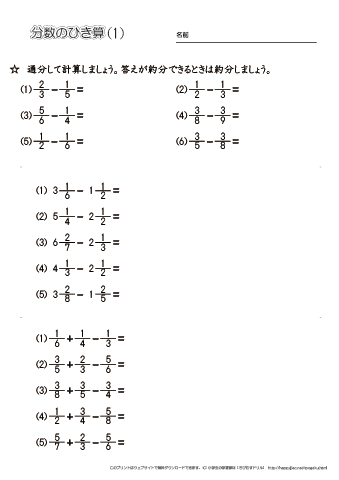



小学5年生の算数 異分母の分数の引き算 問題プリント ちびむすドリル 小学生




小学3年生 算数ドリル 分数2 分母が同じどうしのたし算 プラス パル




分数の足し算 引き算の計算方法 小学生に教えるための分かりやすい解説 数学fun




すきるまドリル 小学5年生 算数 分数のたし算とひき算 無料学習プリント すきるまドリル 無料学習プリント




通分と約分 算数用語集
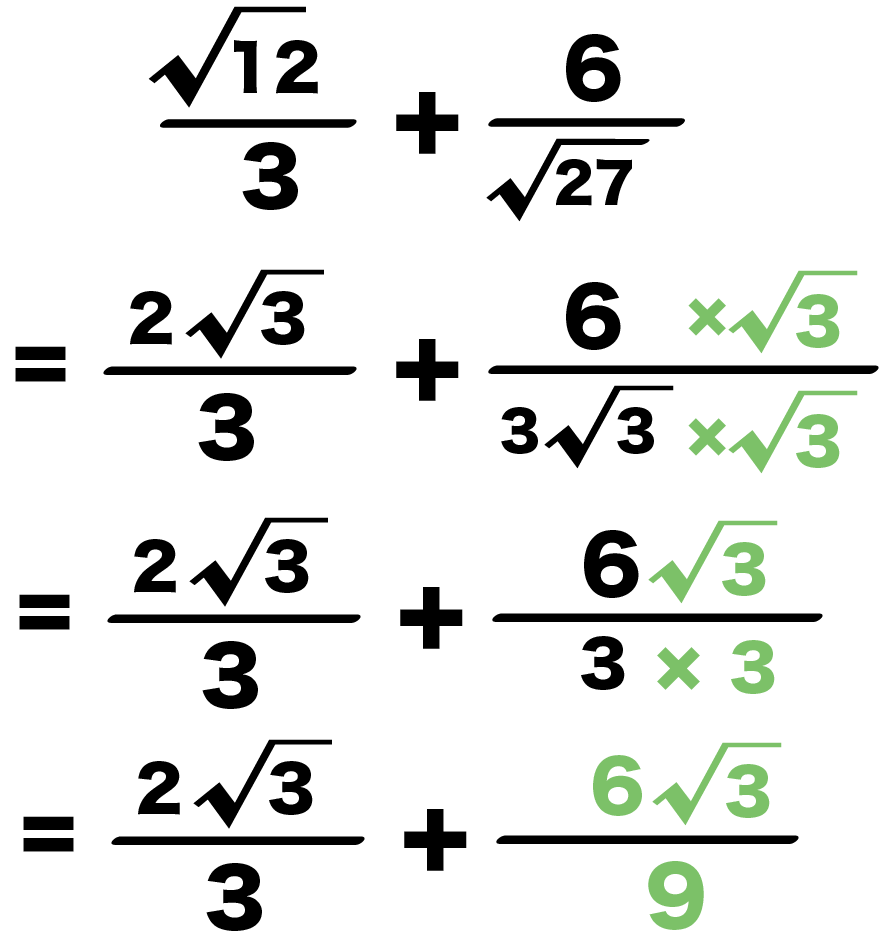



平方根の計算 ルートの分数の足し算 引き算の仕方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




文字が入った分数の足し算や引き算 分子にかっこをつけて通分する 中学や高校の数学の計算問題
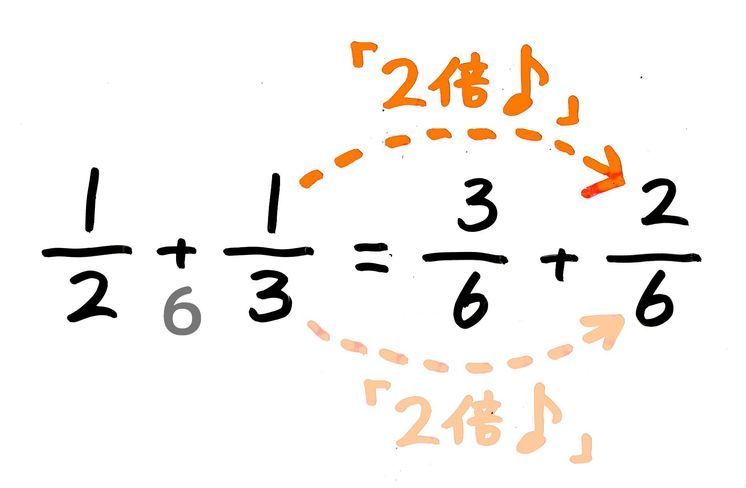



小5 異分母分数の足し算引き算の計算問題のやり方を図解 小6 中学受験生の復習にも そうちゃ式 分かりやすい図解算数 別館
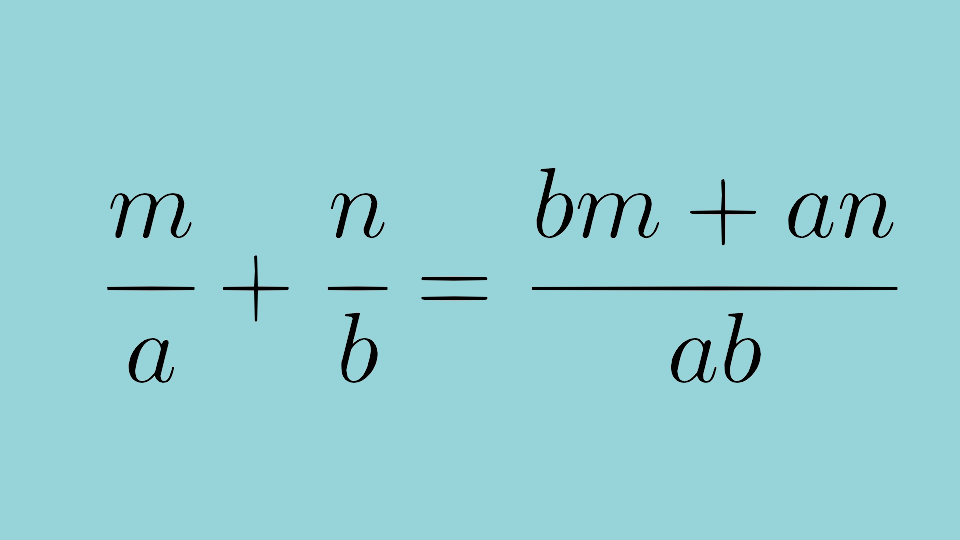



足し算の結果が約分できる2つの既約分数 の条件 オンライン講師ブログ




分数の足し算を覚えよう 数学嫌いな子のための簡単理解法 分かりにくいを分かりやすいに



1




小学校5年 算数 分数のひき算1 分母がちがうひき算 通分 Youtube



分子が足し算 掛け算の分数の約分方法について 約分は小学生の Yahoo 知恵袋




分数の足し算 引き算の計算方法 小学生に教えるための分かりやすい解説 数学fun




分母が違う分数を解く 通分 色とりドリ ママと育児ダイアリー




約分を小学生並みにマスターさせる




簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説




分数の分子に足し算がある場合 約分が出来ないのはなぜですか 分子 数学 教えて Goo
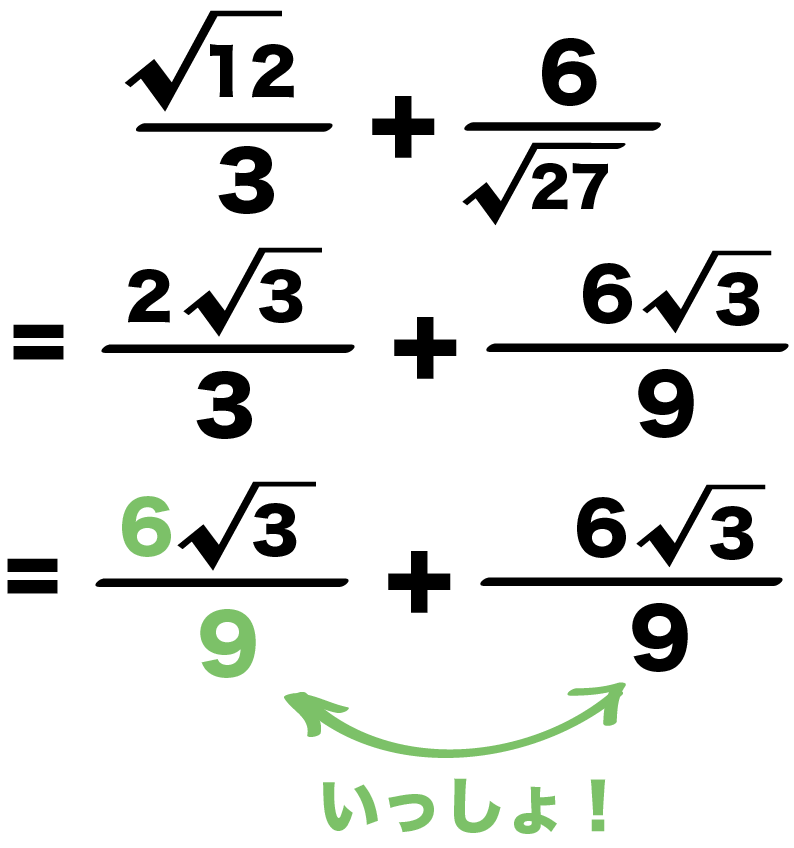



平方根の計算 ルートの分数の足し算 引き算の仕方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




小学3年生 算数 無料問題集 分母が同じ分数の足し算 おかわりドリル
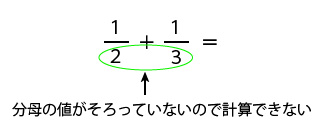



通分と約分 もう一度やり直しの算数 数学




方程式の問題で分数のときは分母を通分すべきなのか 中学や高校の数学の計算問題



異分母の足し算のやり方 大人の学び直し算数 計算のやり方解説 無料




分数の通分の練習問題 計算ドリル 問題集 数学fun




Logの足し算は掛け算で計算するのじゃないんですか なぜここは通分なんですか Clear




小学生の算数 分数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 小学生




分数の足し算で 約分 が発生する条件 Tsujimotterのノートブック
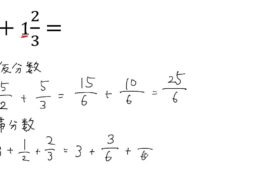



小学校5年算数 5 7 帯分数の足し算 通分あり Cmovie 教育に特化した無料動画サイト シームービー オンライン学習サイト




分数の足し算 引き算の計算方法 小学生に教えるための分かりやすい解説 数学fun




分数の足し算 引き算の計算方法 小学生に教えるための分かりやすい解説 数学fun




帯分数 仮分数 真分数とは 足し算や引き算など計算のやり方を わかりやすく解説




算数 分数の約分のしかた 教え方のコツ なるほど 塾講師が教える教え方のコツ
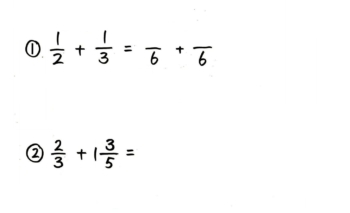



一週間で完成 小学5年生への分数の教え方のコツ 約分 通分 足し算引き算 そうちゃ式 分かりやすい図解算数 別館




帯分数の足し算の計算プリント 分母が異なる問題 全180問無料 算数パラダイス
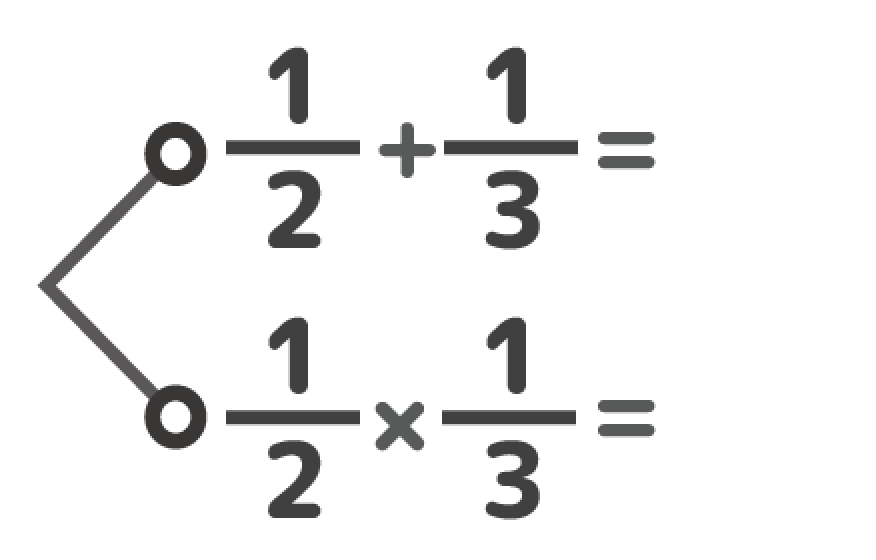



小6への分数の教え方のコツ 計算方法の違いを理解させる かけ算割り算と 算 算 そうちゃ式 分かりやすい図解算数 別館




分数の足し算の計算プリント 分母が異なる問題 全240問無料 算数パラダイス



通分とは 1分でわかる意味 足し算と引き算の問題 最小公倍数との関係



異分母の足し算のやり方 大人の学び直し算数 計算のやり方解説 無料
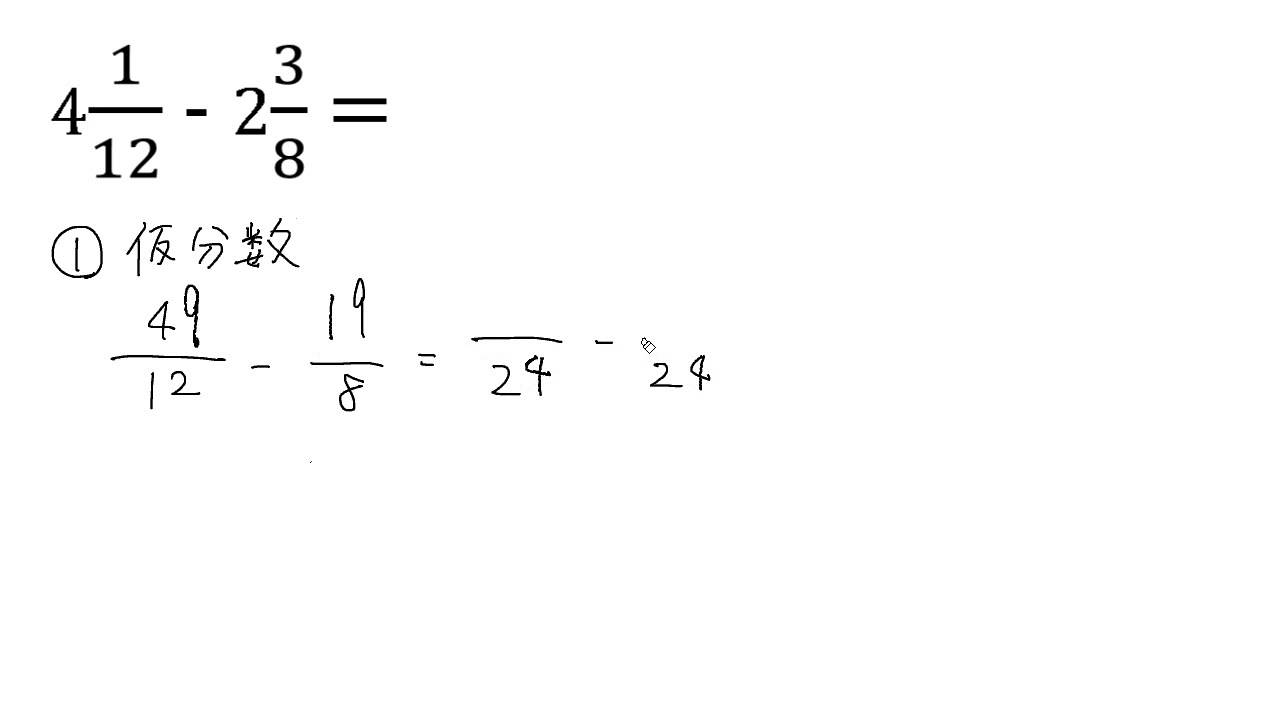



帯分数の引き算 通分あり Youtube




分数の足し算 練習問題 Youtube




分数の足し算や引き算の問題 通分できるかが非常に大切 中学や高校の数学の計算問題
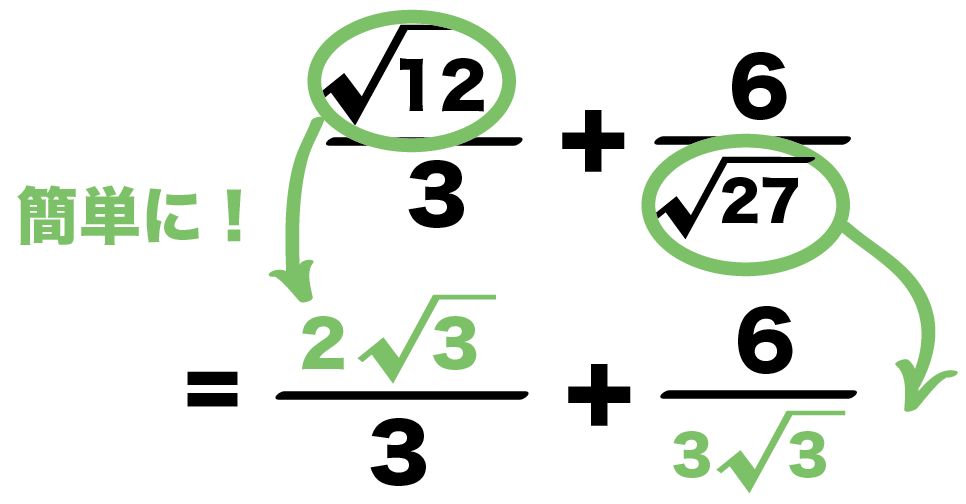



平方根の計算 ルートの分数の足し算 引き算の仕方がわかる5ステップ Qikeru 学びを楽しくわかりやすく
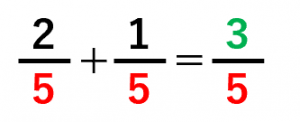



分数の足し算 引き算 具体例で学ぶ数学




分数の足し算の計算プリント 分母が同じ問題 全240問無料 算数パラダイス




帯分数の足し算 通分あり Youtube




小学校5年 算数 分数のたし算2 約分がひつようなたし算 Youtube




仮分数 帯分数 真分数とは 帯分数の掛け算などの応用問題4選も解説 遊ぶ数学



1



異分母の足し算のやり方 大人の学び直し算数 計算のやり方解説 無料



異分母の足し算のやり方 大人の学び直し算数 計算のやり方解説 無料




中1数学 番外編 分数のおさらい 分数の足し算 引き算 すずき なぎさ Note
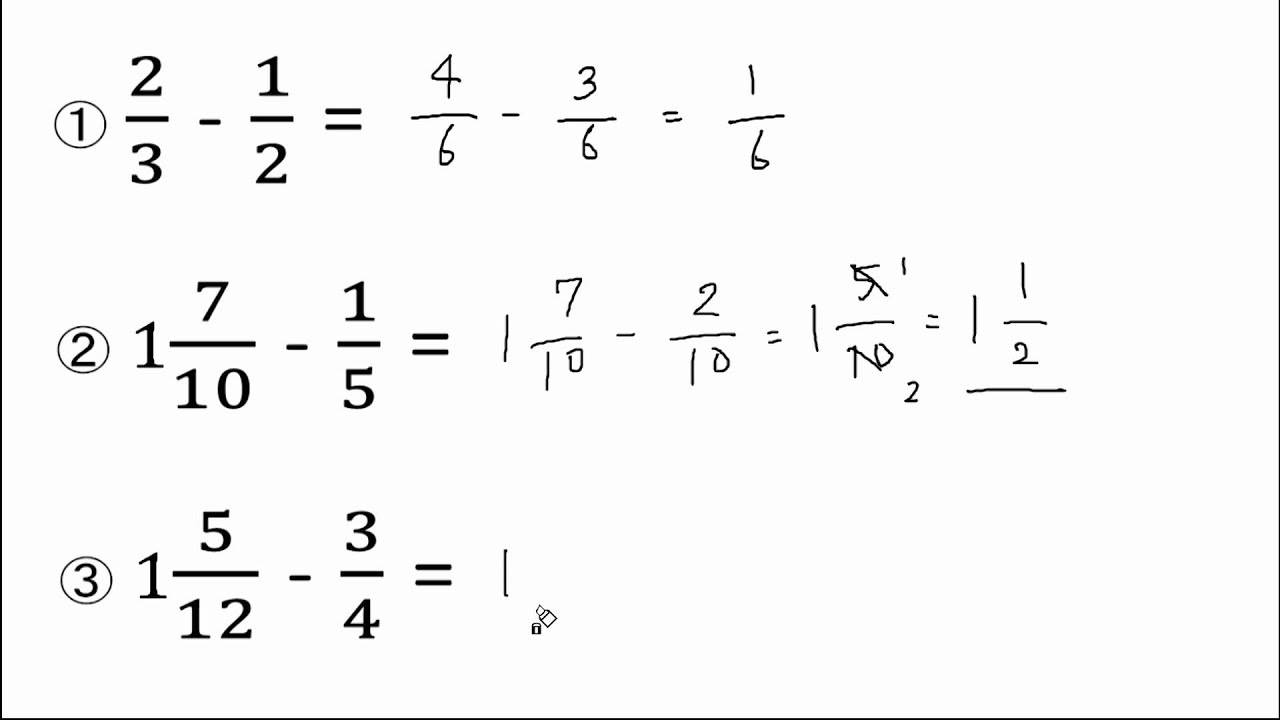



小学校5年 算数 分数のひき算 勉強 Youtube スタディチューブ




分数の引き算 分母が異なる 計算ドリル 問題集 数学fun



ドリルズ 小学5年生 算数 の無料学習プリント3つの分数の足し算 引き算の問題です




約分なしの分数の掛け算の計算のやり方や意味の教え方は みけねこ小学校




分数の足し算 引き算の計算方法 小学生に教えるための分かりやすい解説 数学fun
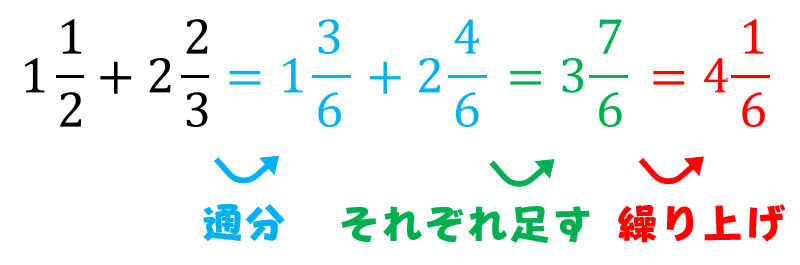



分数の足し算 引き算の計算方法 小学生に教えるための分かりやすい解説 数学fun
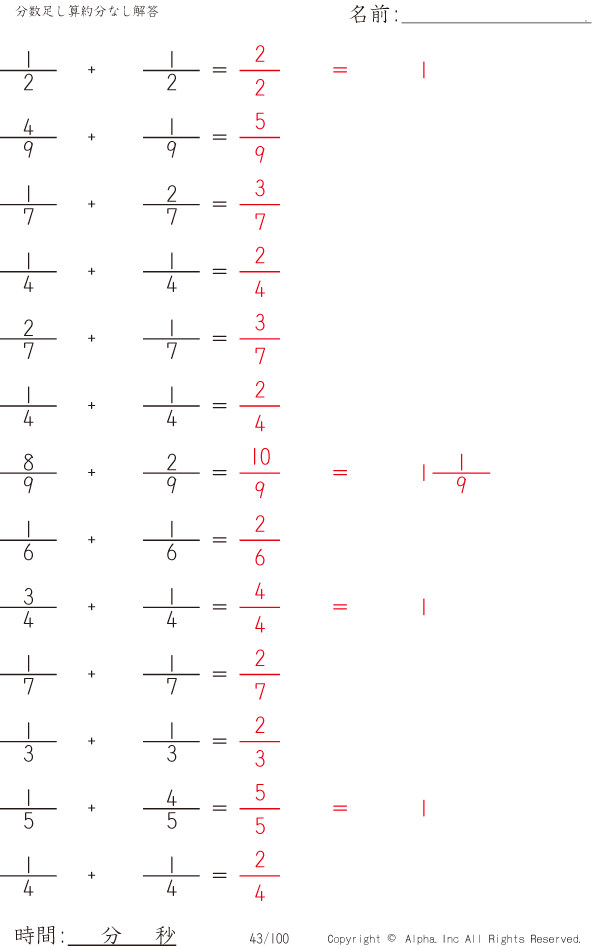



分数足し算約分なし 解答 043 100




分数と整数の足し算引き算が分からなくなってしまいました どなたか途中式や解説お願いい Clear




分数の足し算 分母が異なる 計算ドリル 問題集 数学fun




幼児でも分数の加減乗除を習得




小学5年生向け分数の足し算計算 大きく6パターン




算数 小学校5年生 約分と通分 分数の足し算引き算 Youtube




分数ってなぜ比べにくいの 通分の仕方がわかれば分数の計算も簡単に 中学受験ナビ




小学5年生 算数 無料問題集 分母が違う帯分数の足し算 おかわりドリル
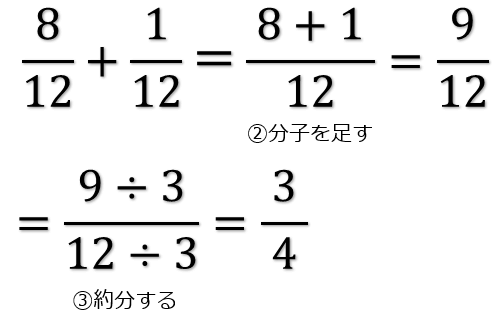



分数の計算まとめ 分母が違う分数の足し算 引き算 掛け算 割り算のやり方 アタリマエ




分数のかけ算 式の中で約分する Youtube




分母が違う分数の足し算 通分して計算する理由は分配法則を考えればわかる 数学の面白いこと 役に立つことをまとめたサイト


