A = 面積 L = 弧の長さ α = 角度 (DEG) α = 角度 (rad) 円 A = 面積 D = 外径 d = 内径 楕円 A = 面積 P = 円周 (近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 大きい円の面積と、大きい円の中にある半円の面積4つ分の差は、 =㎠ よって、 答え ㎠ 面積④ 重なりや移動でできた面積 例題5 長方形と正方形が下の図のように重なっています。色の付いた部分の面積を求めなさい。 解説円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積 弓形の面積(中心角から) 弓形の面積(弓形の半径と高さから) 弓形の面積(弓形の弦長と高さ
円の面積 直径 半径 円周の計算機 公式を使った求め方も紹介 やまでら くみこ のレシピ
円の面積 応用
円の面積 応用-求める面積は、 次の式から求めることができます。 扇形CAOBの面積 + 扇形OBCAの面積 - 菱形AOBCの面積 したがって、 求める面積は、 問 題 2 直径 3cm の円が2つある。 それぞれの中心との距離は である。 重なる部分の面積はいくらか? 球の表面積は半径rの2乗に比例します。 球の表面積の例題1 半径5の円の表面積は? 公式にr=5を代入して 球の表面積の例題2 表面積が36πの球の半径は? 今度は表面積から半径を求める問題なので、公式にS=36πを代入して




円の面積の公式 なぜ半径と円周率で求められるのか を小学生に分かりやすく説明する方法 数学fun
円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積 弓形の面積(中心角から) 弓形の面積(弓形の半径と高さから) 弓形の面積(弓形の弦長と高さ・四角形の面積(4辺と対角の和) 4辺の長さと対角の和から四角形の面積を計算します。 円・扇形の面積 ・円の面積 半径から円の面積と周囲の長さを計算します。 ・扇形の面積 半径と中心角から扇形の面積、円弧の長さ、弦の長さを計算します。 円の面積 円の面積と円周の公式はどっちがどっちだか わからなくなることがありますのでしっかり確実に覚えておくようにしましょう。 円の面積 = 半径 × 半径 × 円周率 弧の面積 まず、円の面積を求めて、そのうちの弧の角度分の面積を知りたいの
円 円 半円 扇形 円周長から面積 四角形 四角形 四角形 4辺と対角線 角パイプ 三角形 三角形 三角形(3辺) 四角形 平行四辺形 ひし形 台形 lc形 l形 c形 円形 パイプ 楕円 長穴 多角形 六角形 八角形 その他 円 円を扇形に切って並べ直してみると 円の面積の公式はご存じの通り、πr 2 である。 πは円周率、rは半径だ。 ではなぜ、この式になるの楕円の面積の計算 小学校の算数で、円の面積を覚えさせられた記憶のある方もいるでしょう。 円の面積は 半径 x 半径 x 円周率 でしたね。 では、楕円の場合はどうでしょうか。 楕円とは、円を縦方向に (または横方向に)伸ばしたものです。 楕円の
円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積 弓形の面積(中心角から) 弓形の面積(弓形の半径と高さから) 弓形の面積(弓形の弦長と高さ円筒の面積と、円の面積の違い 円筒の面積の面積と、円の面積の違いを下記に整理しました。 円筒の面積 ⇒ A=π×(ra 2 -rb 2 ) 円の面積 ⇒ A=π×r 2 円筒の面積は、中が空洞です。空洞部の面積を引いた値が、円筒の面積ですね。 まとめ円Aの半径が分かると、図Cの赤い扇形の面積が分かる。 扇形の面積から黄色い図形の面積を引くと、$\displaystyle \frac{S_{1}}{2}$だ。 ここで、図Bの2つの斜線の三角形は合同なので、面積が等しい。 なので、図Cの黄色い図形と、斜線の図形は面積が等しい。




円の面積の求め方を考えよう 小学校6年生の算数教材から 身勝手な主張



小6算数 円の面積 指導アイデア 2 みんなの教育技術
円 円 半円 扇形 円周長から面積 四角形 四角形 四角形 4辺と対角線 角パイプ 三角形 三角形 三角形(3辺) 四角形 平行四辺形 ひし形 台形 lc形 l形 c形 円形 パイプ 楕円 長穴 多角形 六角形 八角形 その他 円円の面積を求める公式は、次の通りです。 円の面積 = 半径× 半径×314 円の面積 = 半径 × 半径 × 314 円周の長さを出すために、まず円の直径を知る必要があります。 この円の面積が096㎠であることから 円の面積=半径×半径×314=096(㎠) 半径×半径=096÷314= 64 同じ数をかけて64になるのは8。 半径が8cmとわかったので、直径はその2倍の16cm




円の面積 円周の求め方 公式とやり方を解説 小学生向け 中学数学 理科の学習まとめサイト




中学数学 円の面積の求め方 の公式を1発で覚えてしまう裏技 Qikeru 学びを楽しくわかりやすく
円の面積=半径×半径×314 =7×7×314 =cm2 (2)円の面積=半径×半径×314の式から、面積÷314で、 (半径×半径)がわかる。 底面の円の面積は、 5×5×π=25π㎡ 高さは 10cmなので、25π×10=250π㎥ (2) 図より、底面の円の直径が 8cmだから、半径は4cm底面の円の面積は、4×4×π=16π㎡ 高さは 5cmなので、16π×5=80π㎥ ※(2)は直径が与えられていることに注意!半径は直径の半分!円の面積は 半径×半径×円周率=面積 で求めることができます。 半径をr、円周率をπ、面積をSとすると S=πr 2 となります。



多角形の面積で円周率を求める Allisone




File 円の面積 Png Wikimedia Commons
直径Dから面積Aに変換する計算は「A=πD 2 /4」です。 円周率と直径の二乗を掛けて4で割った値です。 また、直径Dと半径rは「r=D/2」の関係です。 よって半径から面積に変換する計算式は「A=πr 2 」です。6年「円の面積」 氏名 1 次の円の面積は何㎠ですか。 ⑴ 半径4cmの円 半径 × 半径 × 314 = 円の面積 式 答え ⑵ 半径8cmの円 式 答え ⑶ 直径14cmの円 直径 ÷ 2 = 半径 式 半径 × 半径 × 314 = 円の面積 答え ⑷ 直径18cmの円 式 答え楕円の面積を求める方法 楕円とは、円を平たく伸ばしたような二次元図形の一種です。幾何の授業で習った人もいるでしょう。楕円の面積は、長半径と短半径の長ささえわかれば、簡単に求めることができます。 楕円の長半径を特定する 長半径とは、楕円の中心から周上の一番遠い点までの



円の面積の公式 算数の公式




円の面積はなぜ P R R なのか 公式の求め方を丁寧に解説 数学の面白いこと 役に立つことをまとめたサイト
公式チェック 円の面積と潤辺の式を確認する。 1 円の面積 右の図の扇形部分の面積に、その上の三角形の面積を加えればよいので まず、扇形の面積を求めると (式-2-1) 次に、三角形の面積を求めると 円の面積は A = πr2 A = π r 2 円周は ℓ = 2πr ℓ = 2 π r 球の体積は V = 4 3 πr3 V = 4 3 π r 3 球の表面積は S = 4πr2 S = 4 π r 2 この式を見比べていて、中学生の時の僕は何か規則性があることに気づきました。 円の面積 A = πr2 A = π r 2 の式において、 r2 r 2 の 2 2 をA=面積 鋭角三角形 鈍角三角形 台 形 不平行四辺形 なお点線にて示すごとく二つの三角形となし、各々の面積を計算し、 その和をもって不平行四辺形の面積を算出してもよい。




小6 算数 小6 旧 円の面積 Youtube



円の面積 2 5
8 rows 円 円 半円 扇形 円周長から面積 四角形 四角形 四角形 4辺と対角線 角パイプ 三角形 三角形 三角形(3辺) 四角形 平行四辺形 ひし形 台形 lc形 l形 c形 円形 パイプ 楕円 長穴 多角形 六角形 八角形 その他 円A=面積 a=面積 a=面積 もし とすれば a=面積 a=面積 もし とすれば a=面積 p=楕円の周囲 a=πab 、pを求める近似式 a=面積 a=面積bcd a=面積 なお点線に示すよう二つの三角形となし 各々の面積を計算しその和をもって 不平行四辺形の面積を算出してもよい =弧の 円の面積の求め方 円の面積を求めるときは 円の面積 = 半径 × 半径 × 円周率 という公式を使います。 たとえば、半径が 3 c m の円の面積は 半径 半径 円周率 半 径 × 半 径 × 円 周 率 = 3 × 3 × 314 = 26 c m 2 と求めることができます。



円積率 雑学のソムリエ
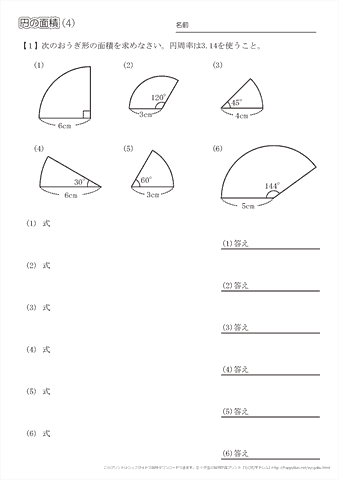



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生
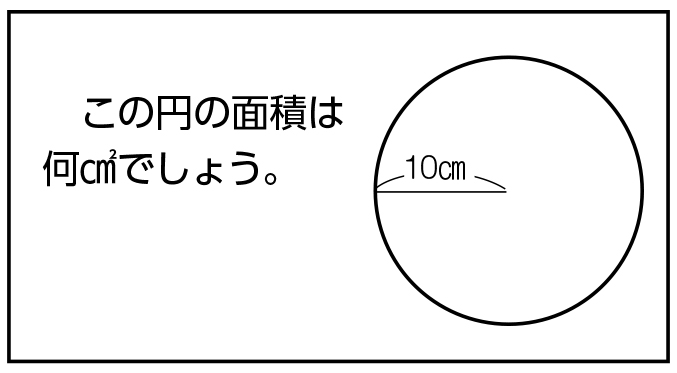
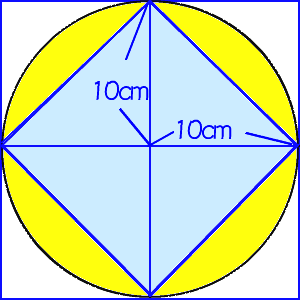
円の面積は、半径を1辺とする正方形の面積の2倍と4倍の間にあることを調べる。 作業的な活動 円の面積の見当を付けて、 1c㎡ の正方形がいくつ分あるか、方眼を用いて調べる。 円を等分して、平行四辺形などの既習の求積可能な図形に変形する。 問題 (正方形、長方形、平行四辺形、台形、ひし形、三角形、円を提示する) 面積の求め方が分かっている図形はどれでしょう。 四角形や三角形は求めることができます。 円はまだ学習していません。 これまでの面積の学習を生かして、円の面積の円の面積のおよその大きさを考えよう 半径10cmの円の外側に正方形を書くと → 上の図のように、円の面積は、1辺10cmの正方形4つ分の面積より小さいことに気づかせます。 円の外側の正方形の面積は、 (10×10)×4=400 です 半径10cm円は、その内側にあります。



小6算数 円の面積 指導アイデア 1 みんなの教育技術




円の面積 練習応用 Youtube
円の面積 ツイート 面積の計算 ・ 正三角形の面積 ・ 三角形の面積 (底辺と高さ) ・ 三角形の面積 (2辺と間の角度) ・ 三角形の面積 (1辺と両端の角度) ・ 三角形の面積 (3辺の長さ)円の面積を求める公式は小学校で習いますが、なぜその公式になるのか?という 疑問 (ぎもん) は、高校2年生で 微分 (びぶん) を学習するまで分かりません!下のリンクでは、図形的に公式を 理解 (りかい) してもらう方法を 紹介 (しょうかい) しています。学習する学年:小学生 1.面積の単位の説明 面積の単位は、みなさんがよく知っているおなじみの (平方メートル)です。 m 2 (平方メートル)は、土地の面積を表す時によく見かける単位ですよね。 面積とは縦軸と横軸の平面の大きさを表す言葉なので、面積を求める時は、たての長さ×
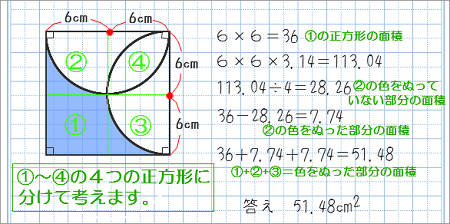



円の面積 その2 家庭学習レシピ
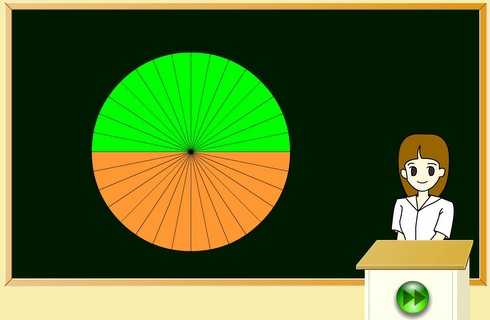



円の面積はなぜ 半径 半径 3 14 なの 一目で理由が分かるサイトが話題に ねとらぼ
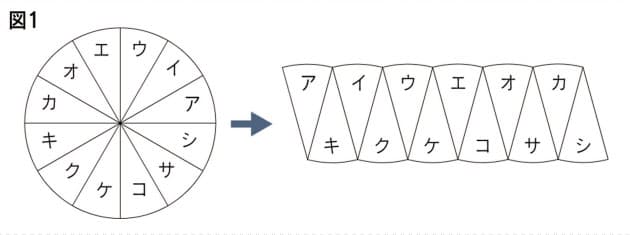



子供に説明できる 円の面積の公式 の証明 Nikkei Style



円の面積と公式 面積計算機




6年算数 円の面積 なぜ 半径 半径 円周率になるのか 解説します Youtube




円の面積 Area Of A Circle Youtube
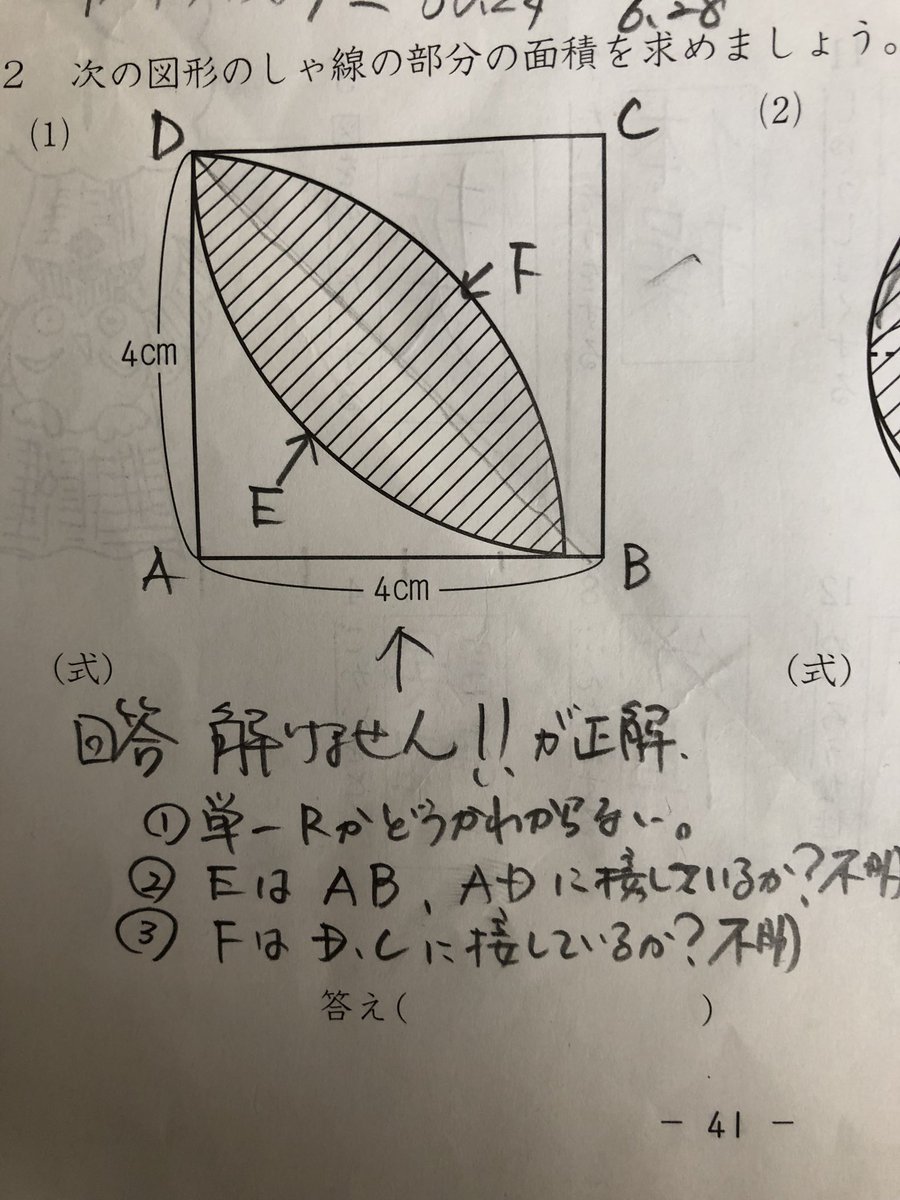



円の面積




勉強しよう数学 円の面積を積分で求める




小6 円 円の面積の求め方 日本語版 Youtube



6年算数 円の面積 1 アニメでわかる教え方
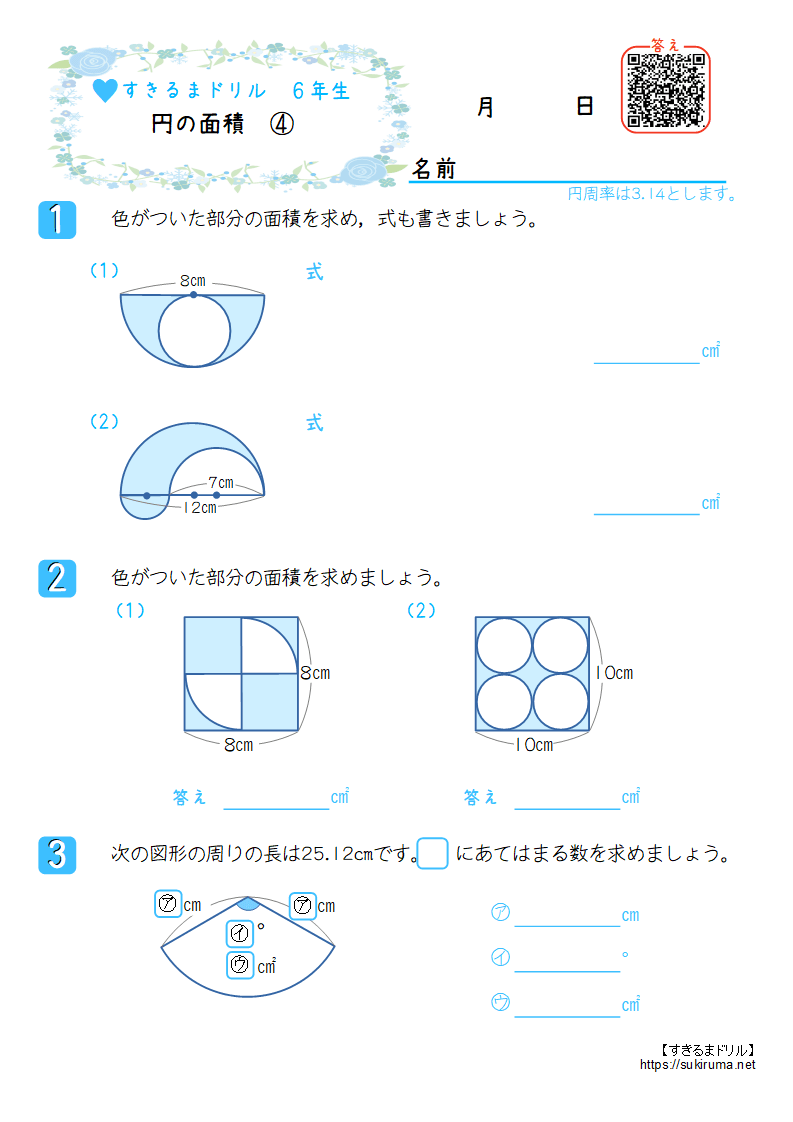



すきるまドリル 小学6年生 算数 円の面積 無料学習プリント すきるまドリル 無料学習プリント




小6 算数 小6 2 円の面積 応用編 Youtube



円の面積を 計算せずに求めるにはどうすればいいですか Quora



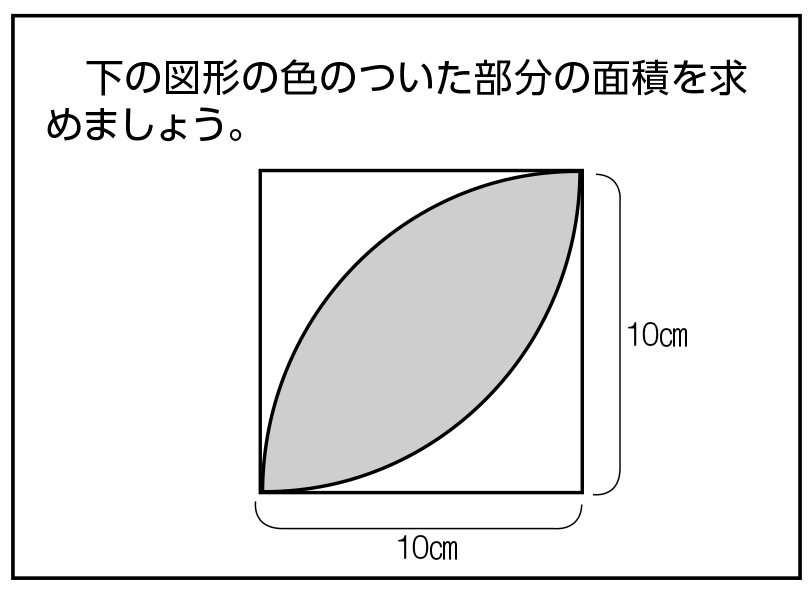
算数 三日月形 半円 の面積の応用問題の答 なるほどの素



円の面積 算数の公式覚えてますか
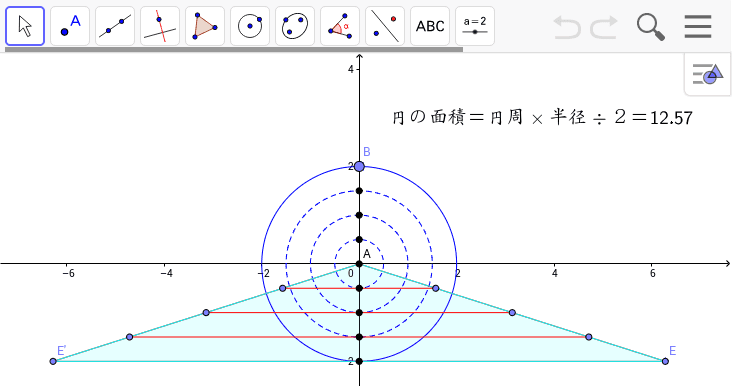



円の面積の求め方 Geogebra




6年算数 円の面積 1 アニメでわかる教え方



円の面積説明器 ヒシエス誠文社 ヒシエス誠文社
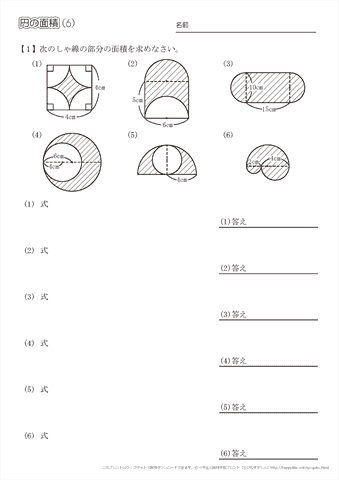



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生




半円や4分の1の円 四分円 の面積を計算する方法 白丸くん



六年生の算数の問題です 円の面積です 写真の を教えてください 式などもよ Yahoo 知恵袋




半径rの円の面積 天ざるの公式ホームページ




円の面積がpr 2になる納得の理由 図形を使った証明 数学の面白いこと 役に立つことをまとめたサイト




円の面積の公式 なぜ半径と円周率で求められるのか を小学生に分かりやすく説明する方法 数学fun




円の面積の求め方と覚えるコツ なぜ半径 半径 3 14になるか アタリマエ
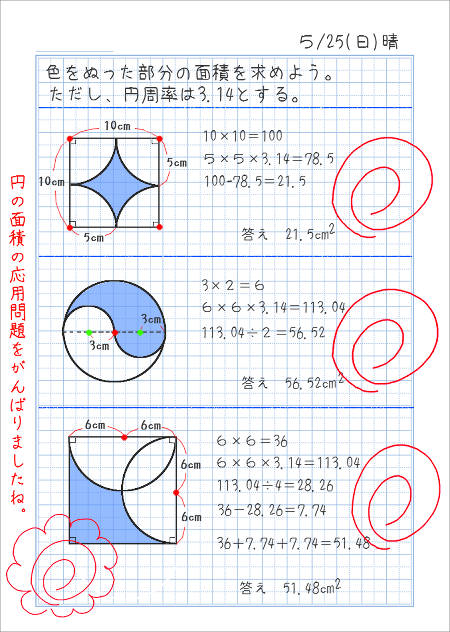



円の面積 その2 家庭学習レシピ
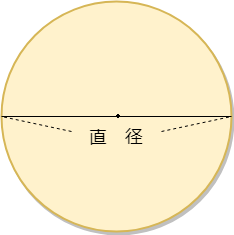



円の面積 円周の求め方 公式 小学生 中学生の勉強
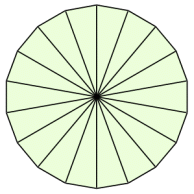



積分 円の面積の再考 大人が学び直す数学
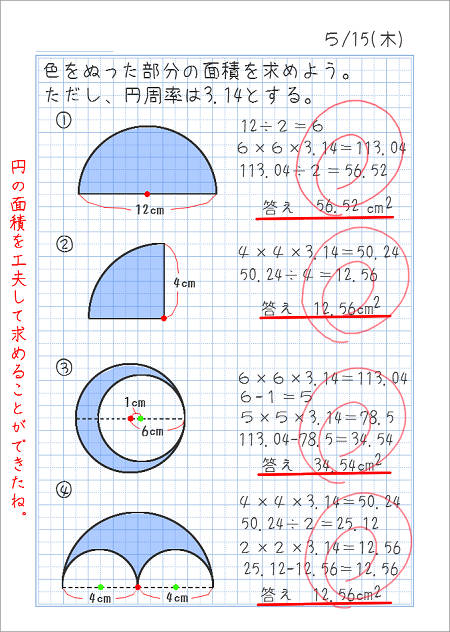



円の面積 その1 家庭学習レシピ
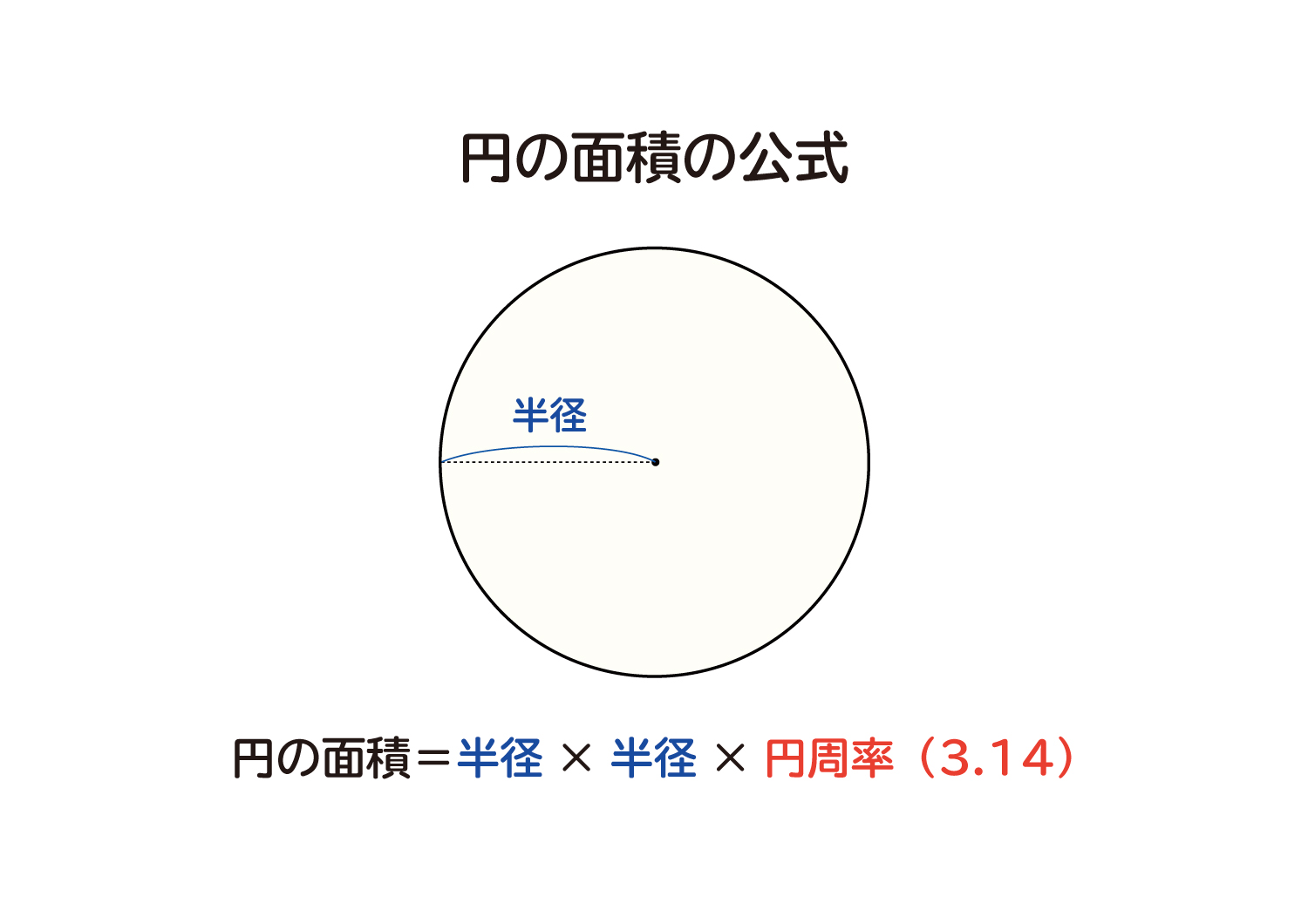



なぜ 円の面積は 半径 半径 円周率 3 14 なのか を説明します おかわりドリル
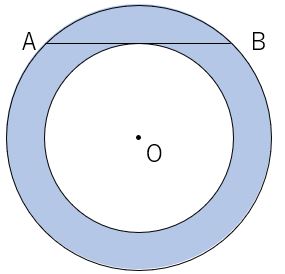



面積 円の面積の変わった求め方の問題 数学の要点まとめ 練習問題一覧




アルゴリズム 2つの円の重なった面積 Teratail




無差別級算数 円の面積 2 解答 受験算数に挑戦
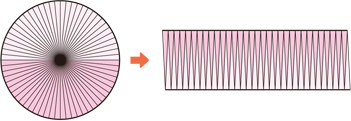



円の面積 算数用語集



1




円の面積の求め方 公式と計算例




平成27年度算数教科書読み比べ 8 円の面積の求め方 わさっきhb



なぜ円の面積 P 半径 半径 なのでしょうか 簡単に証明方法はあるのでしょうか Quora
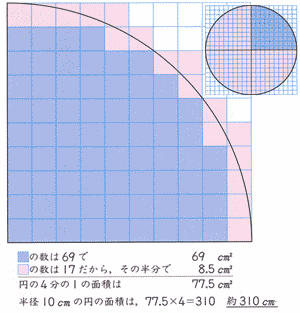



実践記録算数5年




円周率を使って 円の周囲の長さを計算する自主学習ノートを作りましょう 小数のかけ算を使います 5年生の後半から 6年生におすすめの自主学習です 円 半 円 おうぎ形の周囲の長さを計 学習 小学校 算数 中学数学
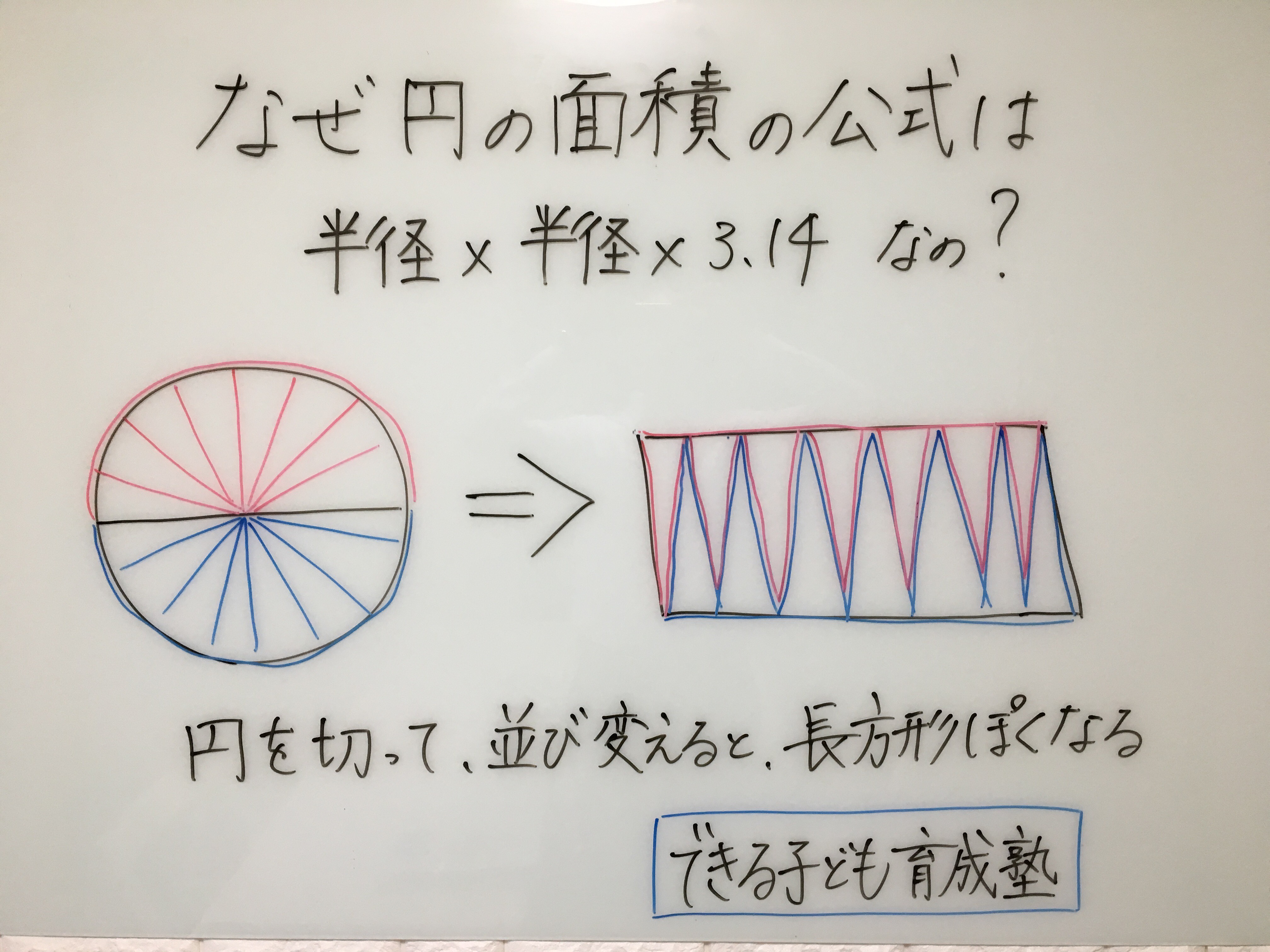



円の面積の求め方 公式 の理由を小学生に教える方法 小岩 個別指導 元小学校教師が教える個別指導塾 できる子ども育成塾 小岩 篠崎の 小学生専門 国語と算数の苦手を克服




すきるまドリル 小学6年生 算数 円の面積 無料学習プリント すきるまドリル 無料学習プリント




円の面積 算数用語集



6年算数 円の面積 2 わかる教え方
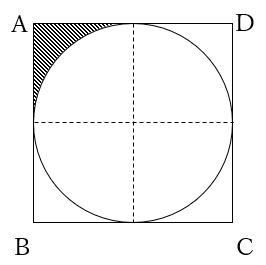



半径の分からない円の面積 中学受験プロ講師ブログ




円の面積の公式 算数の公式




6年生算数ドリル 円
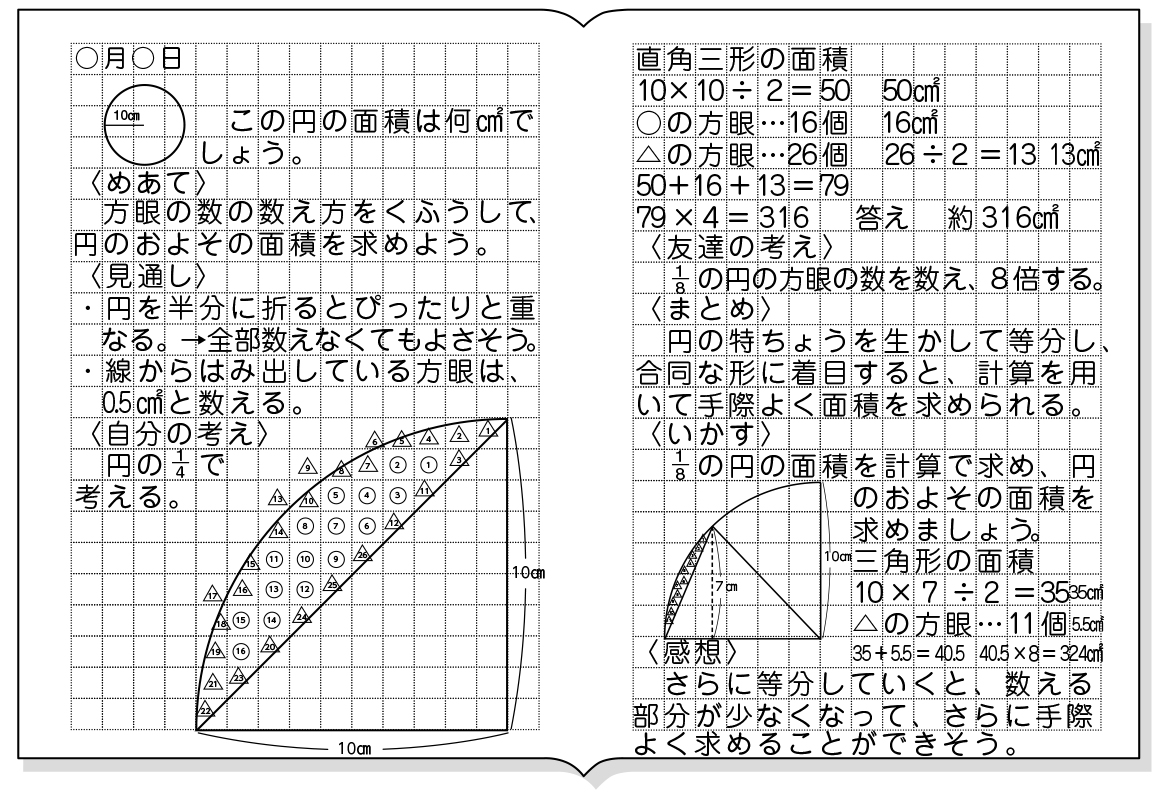



小6算数 円の面積 指導アイデア 1 みんなの教育技術




山と数学 そして英語 小学校算数 円の面積に関する応用問題



じじぃの なぜ半径と半径と3 14を掛けると円の面積になるのか 楽しめる数学 Cool Hira S Diary




円 扇形 の面積 周や弧の長さの公式 数学fun




電気磁気工学を学ぶ 積分と円の面積
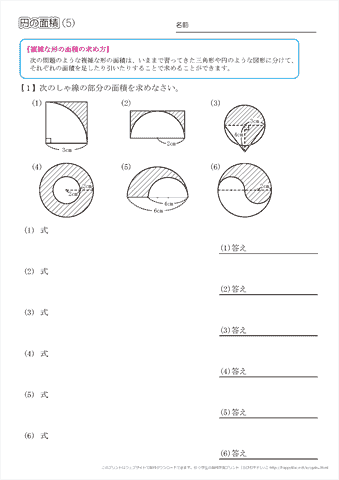



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生
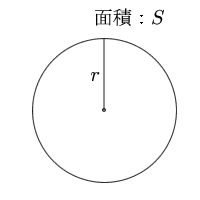



円 面積の計算 計算サイト



6年算数 円の面積 2 わかる教え方



円の面積 直径 半径 円周の計算機 公式を使った求め方も紹介 やまでら くみこ のレシピ




円の面積の求め方 公式と計算例
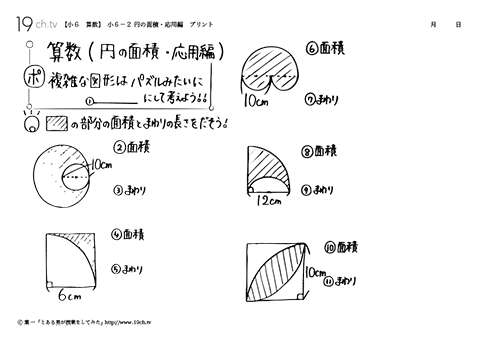



小学6年生の算数 動画 円の面積 応用編の問題 19ch




中学数学 円の面積の求め方 の公式を1発で覚えてしまう裏技 Qikeru 学びを楽しくわかりやすく




円周の求め方と円の面積について アタリマエ
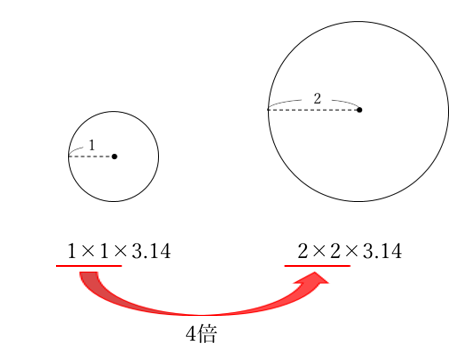



円の相似を利用した面積の計算 中学受験プロ講師ブログ
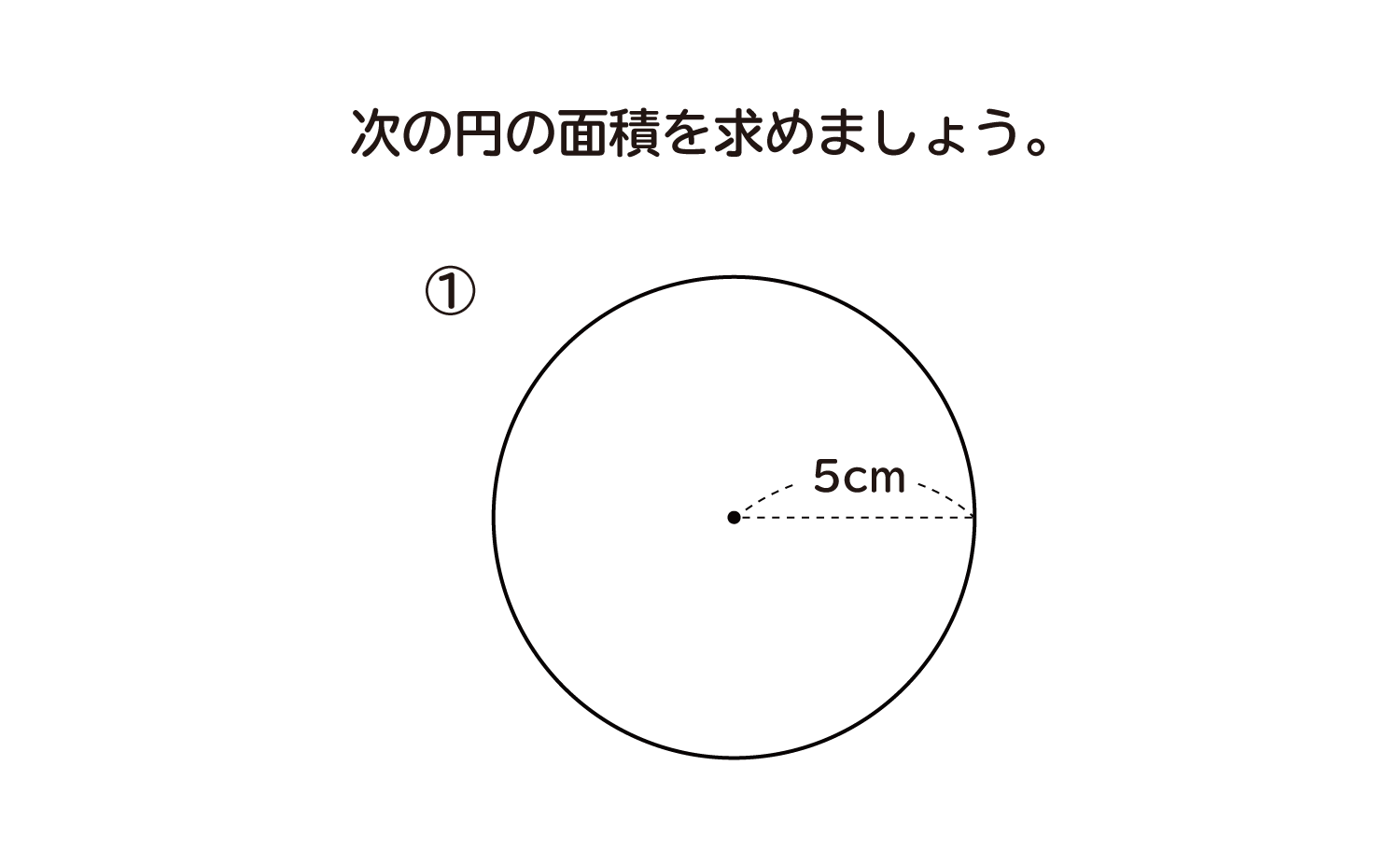



小学6年生 算数 無料問題集 円の面積 おかわりドリル



半径10cmの円の面積を求める公式は10 10 3 14 314m2で Yahoo 知恵袋




円の面積 算数用語集




円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト



1
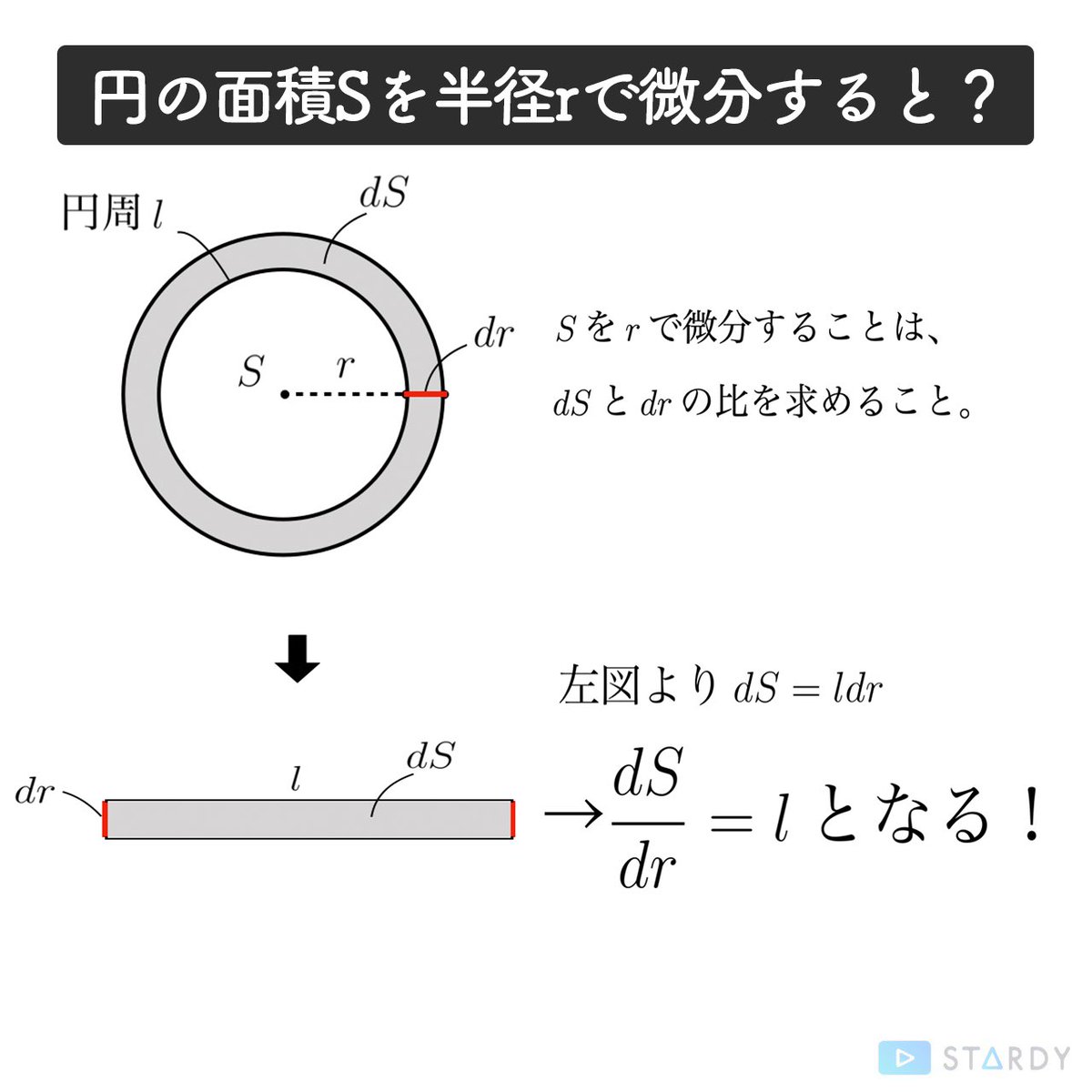



Stardy 実は円の面積を微分すると円周になると知っていましたか T Co Gisrglwseo Twitter
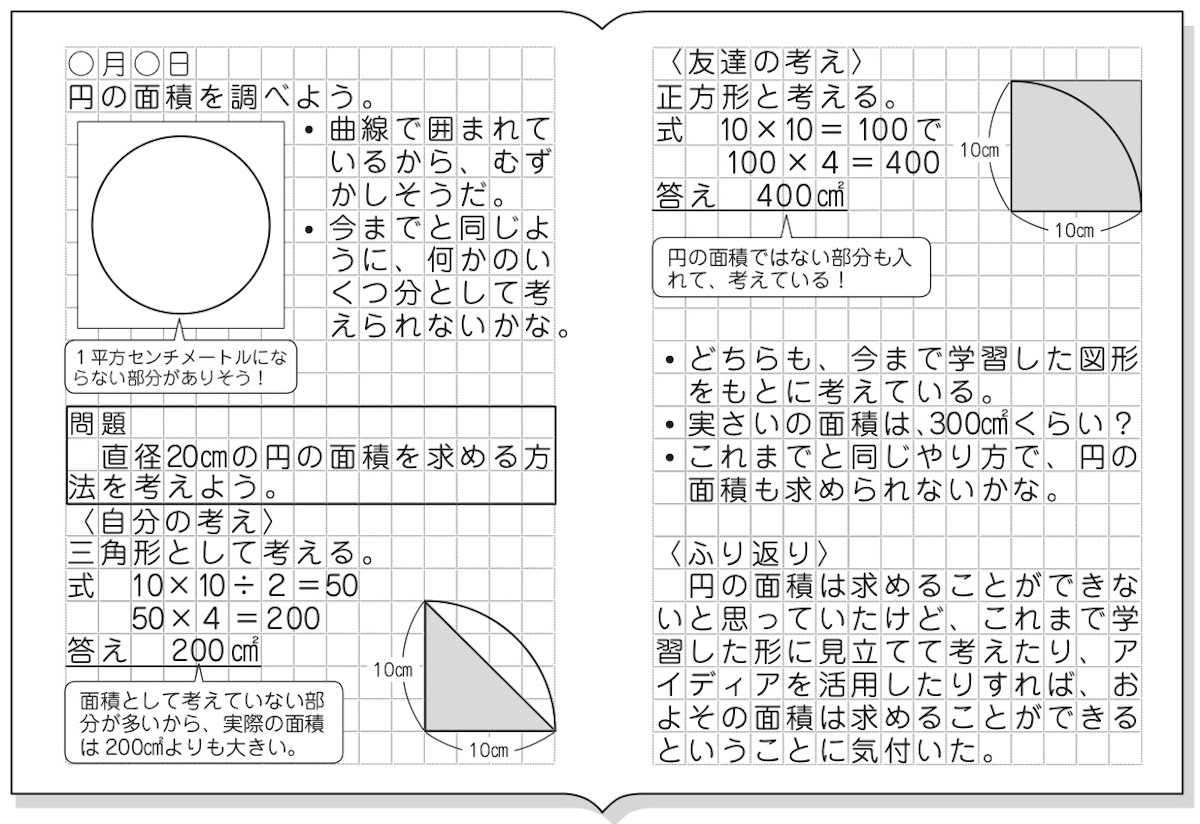



小6算数 円の面積 指導アイデア みんなの教育技術
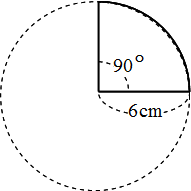



世界一やさしい 円の面積を求める問題の解き方 働きアリ



1
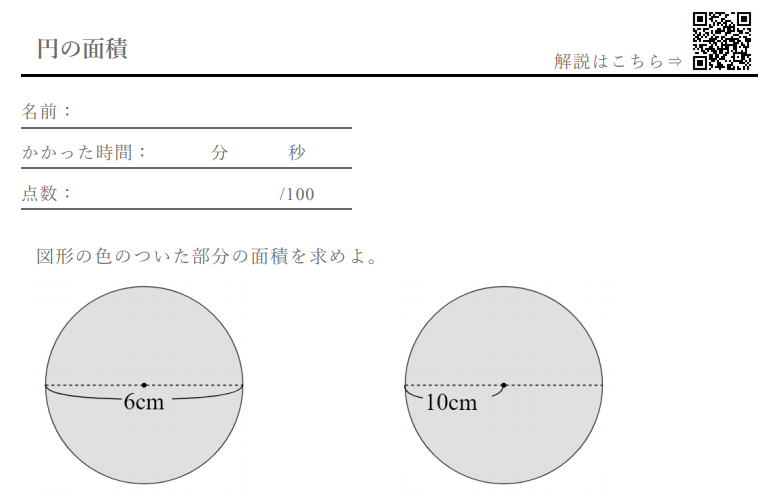



円 の面積 計算ドリル 問題集 数学fun




円の面積の公式 円周の求め方と間違えないようにしよう 中学や高校の数学の計算問題
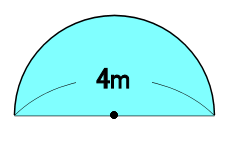



円の面積 半径




円の面積の求め方 公式と計算例




円の面積2 小学校6年生の教科書から 身勝手な主張




6年生算数ドリル 円




小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生
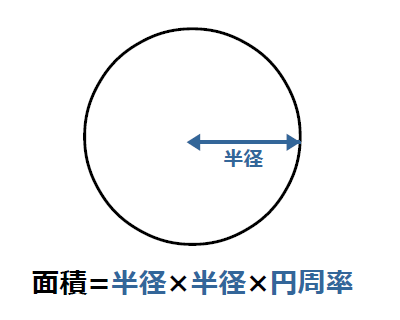



円の面積計算 ゆるゆるプログラミング
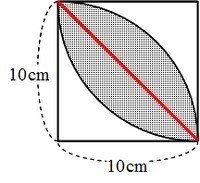



世界一やさしい 円の面積を求める問題の解き方 Shun Ei Note



4 12 半円の重なった部分の面積と周りの長さを求めるには さんすうがく
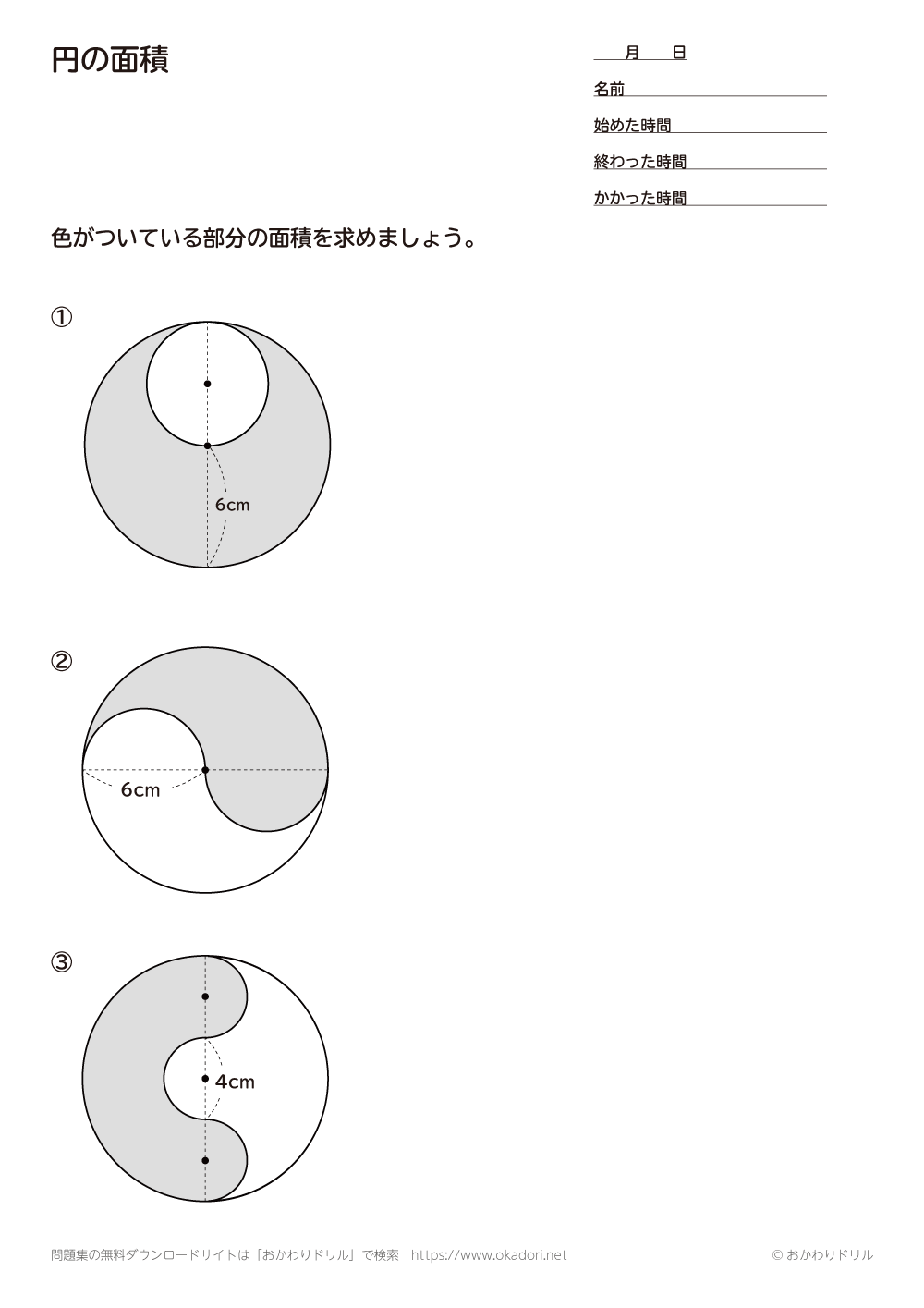



小学6年生 算数 無料問題集 円の面積 おかわりドリル
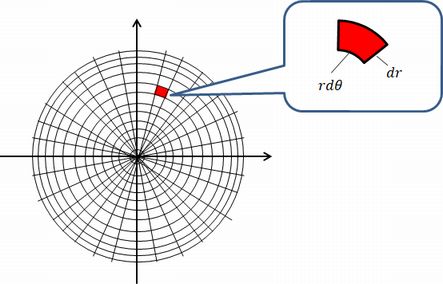



極座標で円の面積を求める方法の補足 おにノート おーにしの物理 数学ノート



気まぐれ Net 図を用いた円の面積の求め方 公式を使わずに
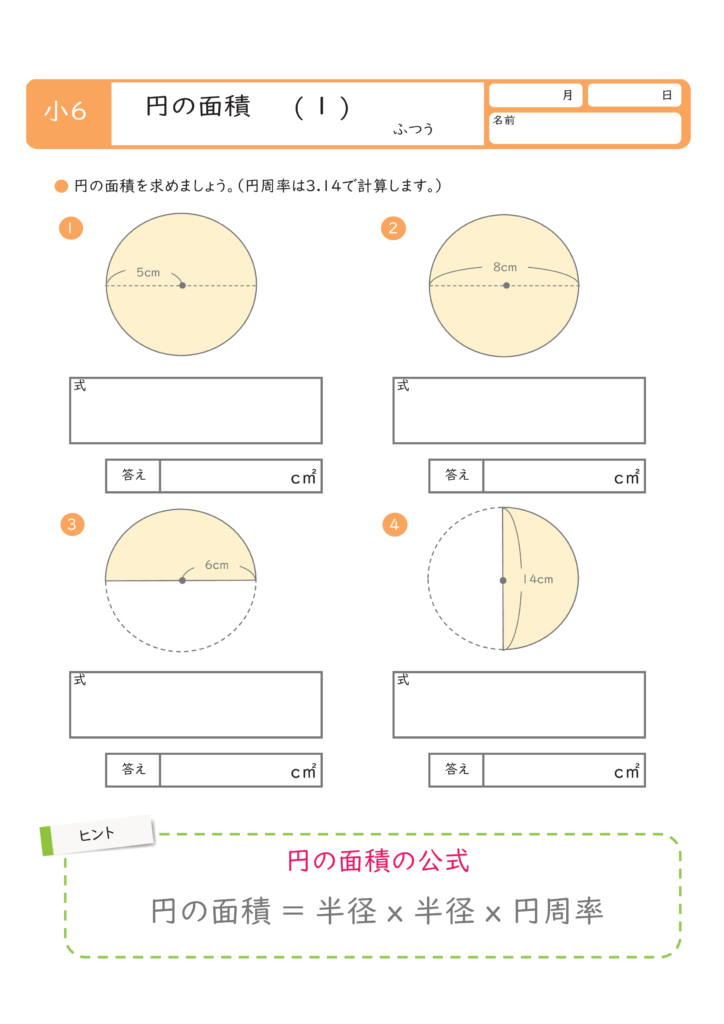



こどもプリント 円の面積 無料プリント




円の面積 小学生 算数のノート Clear




円の面積のもとめ方 小学生 算数のノート Clear
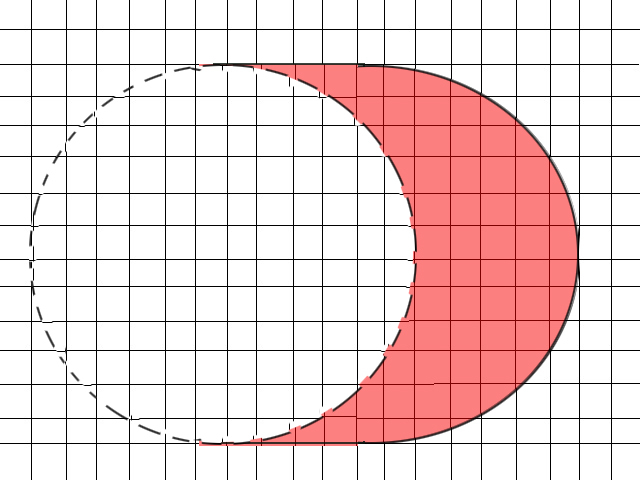



図形の問題 円を5cm横にずらして 移動してできた図形から元の丸を引いた図形の面積を求めてください Jyankquiz



3




円の面積の応用 小学校6年算数より 身勝手な主張
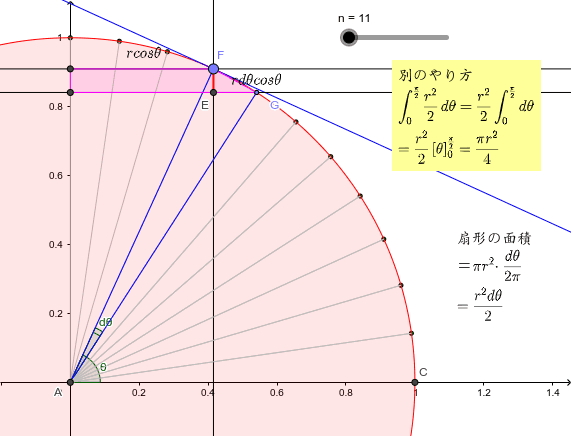



円の面積2 Geogebra


